Giới hạn của dãy số

Giới hạn của dãy số

Chương 4. GIỚI HẠN

A. KIẾN THỨC, VÍ DỤ VÀ BÀI TẬP CĂN BẢN

§1. GIỚI HẠN CỦA DÃY SỐ

1.1. Dãy số có giới hạn 0

Ta nói rằng dãy số ($u_{n}$) có giới hạn là 0 (hay có giới hạn 0) nếu mọi số hạng của dãy số đều có giá trị tuyệt đối nhỏ hơn một số dương nhỏ tuỳ ý cho trước kể từ một số hạng nào đó trở đi. Khi đó ta có thể sử dụng một trong các kí hiệu :

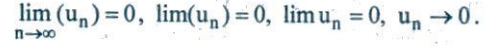
1.2. Một số dãy số có giới hạn 0 thường gặp

d) Dãy số không đổi ($u_{n}$), với $u_{n}$ = 0 có giới hạn là 0;

e) Nếu |q| < 1 thì

Định lí.

Cho hai dãy số ($u_{n}$) và ($v_{n}$).

Nếu |$u_{n}$| $\leq$ $v_{n}$ với mọi n và

1.3. Dãy số có giới hạn

Ta nói rằng dãy số ($u_{n}$) có giới hạn là số thực L nếu

Khi đó, ta có thể sử dụng một trong các kí hiệu:

1.3. Tính chất của dãy số có giới hạn

1.3.1. Giả sử Khi đó,

b) Nếu $u_{n}$ $\geq$ 0 với mọi n thì L $\geq$ 0 và

1.3.2. Giả sử và c là một hằng số. Khi đó :

a) Các dãy số có giới hạn và ta có

b) Nếu M $\neq$ 0 thì dãy số có giới hạn và

Ví dụ 1.

Giải.

1.3.3. Định lí kẹp về dãy số

Cho ba dãy số ($u_{n}$), ($v_{n}$), ($w_{n}$) và số thực L. Nếu $u_{n}$ $\leq$ $v_{n}$ $\leq$ $w_{n}$, với mọi n và thì dãy số ($v_{n}$) có giới hạn và

Ví dụ 2.

Cho với mọi n nguyên dương. Tính

Giải.

Ví dụ 3.

Giải.

Mặt khác, $\forall n\geq 2$, ta có Thật vậy, điều này xảy ra vì ta có biến đổi tương đương sau:

Từ đó suy ra

Vì nên theo định lí kẹp ta có

1.3.4. Định lí

a) Dãy số tăng và bị chặn trên thì có giới hạn.

b) Dãy số giảm và bị chặn dưới thì có giới hạn.

1.4. Tổng của cấp số nhân lùi vô hạn

Cho cấp số nhân $u_{1}$, $u_{2}$, $u_{3}$,... với công bội q thỏa mãn điều kiện $\mid$q$\mid$ < 1. Lúc đó, ta nói cấp số nhân đã cho là lùi vô hạn. Tổng của cấp số nhân đã cho là

Ví dụ 4.

Giả sử số hạng đầu tiên của một cấp số nhân vô hạn là một số nguyên dương, công bội là nghịch đảo của một số nguyên dương và tổng của dãy là 3. Hãy tính tổng của hai số hạng đầu tiên.

Giải.

Gọi $u_{1}$ là số hạng đầu và $\frac{1}{n}$ là công bội của cấp số nhân ấy, thế thì tổng vô hạn của cấp số nhân là :

Vì $u_{1}$, n là số nguyên dương và 0 < $\frac{1}{n}$ < 1 nên (1) cho ta n = 3.

Suy ra $u_{1}$ = 2 và tổng hai số hạng đầu là

1.5. Dãy số dẫn đến vô cực

1.5.1. Dãy số có giới hạn +$\infty$

Dãy số ($u_{n}$) có giới hạn là +$\infty$ nếu kể từ một số hạng nào đó trở đi thì các số hạng của dãy đều lớn hơn một số dương tùy ý cho trước. Khi đó, ta có thể sử dụng một trong các kí hiệu:

1.5.2. Dãy số có giới hạn -$\infty$

Dãy số ($u_{n}$) có giới hạn là -$\infty$ nếu kể từ một số hạng nào đó trở đi thì các số hạng của dãy đều nhỏ hơn một số âm tùy ý cho trước. Khi đó, ta có thể sử dụng một trong các kí hiệu:

Ví dụ 5.

Rõ ràng mọi dãy có giới hạn +$\infty$ hoặc –$\infty$ đều là dãy không bị chặn. Tuy nhiên, điều ngược lại không đúng, nghĩa là một dãy không bị chặn chưa chắc có giới hạn +$\infty$ hoặc -$\infty$. Chẳng hạn, dãy 1, 2, 1, 4, ...,1, 2n,... là dãy không bị chặn nhưng nó lại không có giới hạn vô cùng.

1.5. Một vài quy tắc tìm giới hạn vô cực

Quy tắc 1.