§4. CẤP SỐ NHÂN
4.1. Định nghĩa
Dãy $u_{1}$, $u_{2}$, $u_{3}$, ... được gọi là cấp số nhân với công bội q nếu như ta có $u_{n}$ = $qu_{n-1}$ + q với mọi n = 2, 3, ...
Ví dụ 15.
Dãy 1, 2, 4, 8, 16, 32, - là một cấp số nhân với công bội là 2 và phần tử đầu tiên là 1.
Dãy = 729, 486, 324, 216, 144, 96, 64, ... là một cấp số nhân với công bội là 5 và phần tử đầu tiên là 729.
4.2. Tính chất
1) Nếu dãy số $u_{1}$, $u_{2}$, $u_{3}$, ... là cấp số số nhân thì
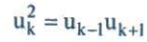với mọi k = 2, 3, ...
2) Nếu dãy số $u_{1}$, $u_{2}$, $u_{3}$, ... là cấp số số nhân với công bội q (q $\neq$ 0) thì số hạng tổng quát của nó là $u_{n}$ = $u_{1}q^{n-1}$.
3) Cho cấp số nhân $u_{1}$, $u_{2}$, $u_{3}$, ... với công bội q (q $\neq$ 1).
Đặt: $S_{n}$ = $u_{1}$ + $u_{2}$ +...+ $u_{n}$. Khi đó, với mọi n $\geq$ 1 ta có :
.png)
4.3. Nhận xét
Sự thay đổi của cấp số nhân tuỳ theo giá trị của công bội.
Chẳng hạn:
Nếu công bội là số dương, các số hạng luôn có dấu cố định.
Nếu công bội là số âm, các số hạng đan dấu giữa âm và dương.
Nếu công bội là 0, mọi số hạng kể từ số thứ hai, bằng 0.
Nếu công bội lớn hơn 1, các số hạng là dãy tăng khi $u_{1}$ > 0 hoặc giảm khi $u_{1}$ < 0.
Nếu công bội là 1, dãy không đổi ($u_{n}$ = $u_{1}$, $\forall$n).
Ví dụ 17.
Cho $a_{1}$, $a_{2}$, $a_{3}$ ... là dãy số dương sao $a_{n+2}$ = $a_{n}a_{n+1}$ với mọi số nguyên dương n. Hãy xác định dãy này nếu nó là một cấp số nhân.
Giải.
Số hạng thứ 2 đến số hạng thứ 5 của dãy đã cho là :
.png)
Nếu dãy số này là một cấp số nhân thì tỉ số các số hạng liên tiếp phải bằng nhau. Suy ra:
.png)
Vậy dãy đã cho là cấp số nhân 1, 1, 1, ... (tất cả các số hạng đều bằng 1).
Ví dụ 18.
Trong một cấp số nhân gồm các số hạng dương, hiệu số giữa số hạng thứ 5 và thứ 4 là 576 và hiệu số giữa số hạng thứ 2 và số hạng đầu là 9. Tìm tổng 5 số hạng đầu tiên của cấp số nhân này.
Giải.
Gọi a là số hạng đầu và q là công bội, ta có:
aq - a = 9 và a$q^{4}$ - a$q^{3}$ = 576.
Do đó
a(q - 1) = 9 (1)
a$q^{3}$(q - 1) = 576. (2)
Chia (2) và (1) vế theo vế ta được : $q^{3}$ = 64 ⇔ q = 4. Suy ra :
.png)
Tổng 5 số hạng đầu tiên là :
.png)
Ví dụ 19.
Trong một cấp số nhân, tổng hai số hạng đầu là 7, tổng sáu số hạng đầu là 91. Tính tổng của bốn số hạng đầu trong cấp số nhân đó.
Giải.
Gọi a và q lần lượt là số hạng đầu tiên và công bội của cấp số nhân. Ta có:
a + aq = a(q + 1) = 7. (1)
.png)
(2)
Chia phương trình (2) cho phương trình (1) ta được :
.png)
Tổng số cần tìm là :
a + aq + a$q^{2}$ + a$q^{3}$ = (a + aq)(1 + $q^{2}$) = 7.4 = 28.
Ví dụ 20.
Cho một cấp số nhân có n số hạng, số hạng đầu tiên là 1, công bội r và tổng là s, trong đó r và s đều khác 0. Tính tổng các số hạng của cấp số nhân mới tạo thành bằng cách thay mỗi số hạng của cấp số nhân ban đầu bằng số nghịch đảo của nó.
Giải.
Cấp số nhân mới có số hạng đầu là 1, công bội $\large \frac{1}{r}$, do đó tổng cần tìm là :
.png)
Mặt khác, .png)
chính là tổng n số hạng của cấp số nhân ban đầu, tức là s, do đó tổng cần tìm là: .png)
Ví dụ 21.
Cho một dãy số gồm 20 số dương có tính chất như sau : bất kì 4 số khác nhau nào của dãy đó cũng lập thành một cấp số nhân. Chứng minh rằng trong dãy 20 số đó phải có ít nhất 5 số bằng nhau.
Giải.
Giả sử ngược lại rằng không xảy ra “trong dãy 20 số đó phải có ít nhất 5 số bằng nhau”. Như thế, trong dãy 20 số đã cho, mỗi số hạng của nó chỉ lặp lại nhiều nhất là 4 lần. Khi đó, trong 20 số dương đó bao giờ ta cũng chọn được 5 số khác nhau a, b, c, d, e.
Không mất tính tổng quát, ta giả thiết a < b < c < d < e.
Khi đó, theo giả thiết ở đề bài, 4 số a, b, c, d lập thành một cấp số nhân và 4 số a, b, c, e cũng lập thành một cấp số nhân. Do đó e/c = c/b = d/c, nên e = d. Điều này mâu thuẫn với giả thiết e $\neq$ d.
Điều mâu thuẫn trên chứng tỏ rằng trong 20 số dương của dãy nhất định phải có ít nhất 5 số bằng nhau.
Nhận xét.
Bài toán trên chỉ là trường hợp đặc biệt của bài toán sau, các bạn có thể chứng minh nó một cách hoàn toàn tương tự:
Cho một dãy số gồm 4n số dương có tính chất : 4 số khác nhau bất kì của dãy lập thành một cấp số nhân. Chứng minh rằng, trong trường hợp đó, trong dãy số phải có ít nhất n số bằng nhau.
BÀI TẬP
3.11. Cho ba số thực a, b, c khác 0. Chứng minh rằng nếu a, b, c theo thứ tự đó lập thành cấp số nhân với công bội q $\neq$ 0 thì ba số .png)
theo thứ tự đó cũng lập thành cấp số nhân.
3.12. Giả sử a, b và c là một cấp số nhân với 1< a < b < c và n là một số nguyên lớn hơn 1. Xét dãy số A, B, C, trong đó:
$n^{A}$ = a, $n^{B}$ = b, $n^{C}$ = c.
Có nhận xét gì về dãy số A, B, C ?
HƯỚNG DẪN GIẢI
3.11. HD: Ba số .png)
theo thứ tự đó cũng lập thành cấp số nhân công bội $\large \frac{1}{q}$
3.12. Ta có :
ac = $b^{2}$ ⇒ $n^{A}n^{C}$ = $n^{2B}$ ⇒ $n^{A+C}$ = $n^{2B}$ ⇒ A + C = 2B.
Vậy dãy số A, B, C là cấp số cộng.