Phương pháp quy nạp toán học

Chương 3. DÃY SỐ - CẤP SỐ CỘNG - CẤP SỐ NHÂN

A. KIẾN THỨC, VÍ DỤ VÀ BÀI TẬP CĂN BẢN

§1. PHƯƠNG PHÁP QUY NẠP TOÁN HỌC

Để chứng minh mệnh đề chứa biến A(n) đúng với mọi giá trị dương n $\geq$ p, với p là số nguyên dương, ta tiến hành hai bước:

Bước 1 (bước cơ sở). Chứng minh rằng A(n) đúng khi n = 1.

Bước 2 (Bước quy nạp). Với số nguyên dương tuỳ ý k (k $\geq$ p), ta giả sử A(n) đúng khi n = k (giả thiết quy nạp). Khi đó, ta sẽ chứng minh rằng A(n) đúng khi n = k + 1.

Ví dụ 1.

Số Fermat là số có dạng

Với n = 0, $F_{0}$ = 3; n = 1, $F_{1}$ = 5; n = 2, $F_{2}$ = 17, ... nhà toán học Pháp Fermat đã cho rằng mọi số $F_{n}$ đều là số nguyên tố. Tuy nhiên điều này không đúng vì với n = 5, ta có

Đây là hợp số.

Dùng phương pháp quy nạp, hãy chứng minh rằng với mọi số nguyên dương n, ta có

Giải.

• Với n = 1, $F_{0}$ = 3, $F_{1}$ = 5 ⇒ $F_{0}$ = $F_{1}$ - 2.

Vậy công thức đúng khi n = 1.

• Giả sử kết quả đúng với k, tức là Ta sẽ chứng minh kết quả đúng với k + 1. Từ giả thiết quy nạp, ta suy ra

Ta lại có

Vậy Kết quả đúng với k + 1.

Theo nguyên lí quy nạp kết quả đúng với mọi số nguyên dương k.

Ví dụ 2. Chứng minh rằng với mọi số tự nhiên n > 3, ta có $3^{n}$ > $2^{n}$ + 7n.

Giải.

Ta kiểm tra được bất đẳng thức đúng với n = 4. Thật vậy, vế trái bằng $3^{4}$ = 81, vế phải bằng $2^{4}$ + 7.4 = 16 + 28 = 44.

Giả sử bất đẳng thức đúng với k, tức là $3^{k}$ > $2^{k}$ + 7k. Khi đó:

Vậy bất đẳng thức đúng với k + 1, suy ra điều phải chứng minh.

Ví dụ 3.

Cho a, b, c là số đo 3 cạnh của một tam giác vuông với c là cạnh huyền. Chứng minh rằng:

Giải.

Với n = 1, theo định lí Pythagore ta có: nên bất đẳng thức đã cho đúng (xảy ra dấu bằng).

Giả sử với n = k ta có

Ta sẽ chứng minh: Ta có:

Vậy bất đẳng thức đã cho đúng với n = k +1 . Do đó, bất đẳng thức đúng với mọi n $\geq$ 1.

Ví dụ 4.

Chứng minh rằng với mọi số nguyên dương n, $4^{n}$ + 15n - 1 là số chia hết cho 9.

Giải.

Với n = 1 ta có $4^{1}$ + 15.1 - 1 = 18. Vậy $4^{n}$ + 15n - 1 là số chia hết cho 9 khi n = 1.

Giả sử $4^{n}$ + 15n - 1 là số chia hết cho 9 với n = k, ta có :

$4^{k}$ + 15k - 1 $\vdots$ 9 ⇒ $4^{k}$ + 15k - 1 = 9m (m $\in$ Z) ⇒ $4^{k}$ = 9m + 1 - 15k.

Với n = k + 1, ta có:

$4^{k+1}$ + 15(k + 1) -1 = 4.$4^{k}$ + 15k + 14.

Thay $4^{k}$ = 9m + 1 - 15k từ trên vào, ta được

$4^{k+1}$ + 15(k + 1) - 1 = 4(9m + 1 - 15k) + 15k + 14

= 36m - 45k + 18 = 9(4m - 5k + 2).

Vậy $4^{n}$ + 15n - 1 là số chia hết cho 9 khi n = k + 1.

Theo nguyên lí quy nạp, $4^{n}$ + 15n - 1 là số chia hết cho 9 với mọi n $\geq$ 1.

Ví dụ 5.

Chứng minh $2^{3^{n}}$ + 1 chia hết cho $3^{n}$ với mọi số tự nhiên n.

Giải.

Ta chứng minh bằng quy nạp. Trường hợp n = 0 đúng vì

$2^{3^{0}}$ + 1 = 3 chia hết cho $3^{0}$ = 1.

Giả sử phát biểu trên đúng với k, tức là ta có $2^{3^{k}}$ + 1 = A.$3^{k}$, với A là số nguyên. Lúc đó,

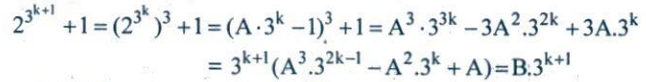
suy ra phát biểu trên cũng đúng với k + 1.

Từ đó, ta có điều phải chứng minh.

BÀI TẬP

3.1. a) Chứng minh rằng với mọi số tự nhiên n $\geq$ 3 ta có

$2^{n}$ > 2n + 1.

b) Chứng minh

c) $\forall n\geq 1$, chứng minh:

3.2. Chứng minh rằng với mọi số tự nhiên n, số $3^{2^{4n+1}}$ + 2 chia hết cho 11.

3.3. (Thi chọn học sinh giỏi Toán PT, ĐH Winconsin, USA, 2000)

Nếu n > 1 là một số nguyên và giả sử

Chứng minh rằng

HƯỚNG DẪN GIẢI

3.1. a) Với n = 3 ta có $2^{3}$ > 2.3 + 1. Giả sử bất đẳng thức đúng với n = k, nghĩa là: $2^{k}$ > 2.k + 1. Ta phải chứng minh bất đẳng thức đúng với n = k + 1, nghĩa là

$2^{k+1}$ > 2.(k + 1) + 1.

Ta có

$2^{k+1}$ = 2.$2^{k}$ > 2.(2k + 1) ⇒ $2^{k+1}$ > 4k + 2 > 2k + 3 = 2(k + 1) + 1.

Vậy bất đẳng thức đúng với mọi n $\geq$ 3.

b) Với n = 2, bất đẳng thức đúng, vì

Giả sử bất đẳng thức đúng với n = k, nghĩa là

Ta chứng minh bất đẳng thức đúng với n = k + 1, nghĩa là ta phải chứng minh Ta có:

Vậy bất đẳng thức đã cho đúng với mọi n > 1.

c) Với n = 1, ta có: 1 > 2$\sqrt{2}$ – 2 ⇔ 3 > 2$\sqrt{2}$ (BĐT đúng).

Giả sử BĐT đúng với n = k, nghĩa là:

Ta chứng minh:

Ta có:

Để có (1) ta chứng minh:

Ta có (2) tương đương với

Bất đẳng thức cuối cùng luôn luôn đúng nên ta có (2).

Từ đó suy ra bất đẳng thức (1) đúng, tức là bất đẳng thức đã cho đúng với n = k + 1.

Vậy bất đẳng thức đã cho đúng với mọi n $\geq$ 1.

3.2. Với n = 0 ta có $3^{2^{1}}$ + 2 = 11$\vdots$11.

Giả sử phát biểu đúng với n = k, tức là : $3^{2^{4k+1}}$ + 2$\vdots$11.

Với n = k + 1 ta có:

Ta có (vì 16 là số chẵn). Hơn nữa, theo giả thiết quy nạp:

Mặt khác:

Vậy $3^{2^{4n+1}}$ + 2$\vdots$11 với mọi số tự nhiên n.

3.3. Trước tiên, ta sẽ chứng minh

Bất đẳng thức này đúng với n = 1, vì 2$\sqrt{2}$ - 2 < 1. Giả sử bất đẳng thức đúng với n, tức là 2$\sqrt{n+1}$ - 2 < $S_{n}$, khi đó:

Vậy, theo nguyên lí quy nạp, ta có bất đẳng thức thứ nhất.

Ta cũng dùng quy nạp để chứng minh bất đẳng thức thứ hai. Dễ thấy $S_{n}$ < 2$\sqrt{n}$ - 1 đúng khi n = 2. Giả sử bất đẳng thức này đúng với n > 1, ta có