§2. HOÁN VỊ, CHỈNH HỢP VÀ TỔ HỢP
2.1. Hoán vị
Một hoán vị của một tập hợp gồm n phần tử là một cách sắp xếp các phần tử của tập hợp này theo một thứ tự nào đó.
Số hoán vị của n phần tử là n! = n(n-1)(n-2)...2.1.
Ví dụ 6.
Có thể lập bao nhiêu số gồm 8 chữ số từ các số 1, 2, 3, 4, 5, 6, trong đó chữ số 1 và 6 có mặt 2 lần còn các chữ số khác có mặt đúng một lần?
Giải.
Ta kí hiệu chữ số 1 và 6 xuất hiện lần hai là 1' và 6'. Vậy mỗi số được chọn là 1 hoán vị của tập hợp gồm 8 phân tử: 1, 1', 2, 3, 4, 5, 6, 6'. Nhưng nếu đếm như vậy sẽ thừa 2!.2! lần do 1' và 6' cũng chính là chữ số 1 và 6. Vậy có $\large \frac{8!}{2!2!}$ = 10.080 số tất cả.
Ví dụ 7.
Một tổ học sinh có 5 nam và 5 nữ xếp thành 1 hàng dọc.
a) Có bao nhiêu cách xếp khác nhau ?
b) Có bao nhiêu cách xếp sao cho không có học sinh cùng giới tính đứng kề nhau ?
Giải.
a) Có 10! cách xếp khác nhau
b) Có 2 trường hợp:
+ Học sinh nam đứng đầu : Khi đó, 5 học sinh nam sẽ đứng ở các vị trí thứ 1, 3, 5, 7, 9 và 5 học sinh nữ sẽ đứng ở các vị trí thứ 2, 4, 6, 8, 10. Có 5! cách sắp xếp 5 học sinh nam vào các vị trí và cũng có 5! cách sắp xếp 5 học sinh nữ vào các vị trí như đã nói.
Theo quy tắc nhân, có 5!.5! cách tất cả.
+ Học sinh nữ đứng đầu : Tương tự, ta cũng có 5!5! cách.
Theo quy tắc cộng ta có 2.$(5!)^{2}$ = 28800 cách.
Ví dụ 8.
Cho các chữ số 0, 1, 2, 3, 4 và 5. Từ các chữ số đã cho ta lập được bao nhiêu số chia hết cho 9, biết rằng số này có 3 chữ số và 3 chữ số đó khác nhau từng đôi một ?
Giải.
Ta có các trường hợp:
1 + 3 + 5 = 2 + 3 + 4 = 4 + 5 + 0 = 9.
Có 3 trường hợp và trong mỗi trường hợp có 3! hoán vị của 3 phần tử.
Như thế, có 3.3! = 18 số. Tuy nhiên, có 2 số có số 0 ở số hạng đầu, đó là 045 và 054. Vậy có tất cả 18 – 2 = 16 số.
Ví dụ 9.
Với n và a là các số nguyên dương, kí hiệu $n_{a}$! là số định bởi
$n_{a}$! = n(n - a)(n - 2a)(n - 3a)...(n - ka),
trong đó, k là số nguyên lớn nhất sao cho n > ka. Hãy tính thương số
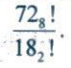
Nhận xét. Theo định nghĩa trên, n! là trường hợp a = 1.
Thật vậy, khi a = 1 thì số nguyên k lớn nhất sao cho n > ka là số k = (n - 1). Do đó :
$n_{1}$! = n(n - 1)(n - 2.1)(n - 3.1)...(n - (n - 1).1) = n(n - 1)(n - 2)(n - 3)...1 = n!.
Giải.
Ta có : $72_{8}$! = 72.64.56.48.40.32.24.16.8 = $8^{9}$(9!)
$18_{2}$! = 18.16.14.12.10.8.4.2 = $2^{9}$(9!)
Do đó: .png)
2.2. Chỉnh hợp
Cho 1 $\leq$ k $\leq$ n.
Một cách sắp xếp k phần tử của tập n phần tử gọi là một chỉnh hợp chập k của n.
Số chỉnh hợp không lặp chập k của n được kí hiệu là $A_{n}^{k}$.
Ta có công thức $A_{n}^{k}$ = n(n - 1)...(n – k + 1).
Nhận xét.
a) Một hoán vị của một tập hợp n phần tử là một chỉnh hợp chập n của n phần tử. Gọi $P_{n}$ là số hoán vị của n phần tử thì
$P_{n}$ = $A_{n}^{n}$ = n!
b) Công thức tính $A_{n}^{k}$ đã được chứng minh ở sách giáo khoa. Tuy nhiên, ở đây, ta có thể lí luận như sau : Để tạo một chỉnh hợp k phân tử, ta có thể lấy ra một chỉnh hợp k - 1 phần tử rồi ghép với một trong số (n - k + 1) phần tử còn lại. Từ lí luận này ta có:
.png)
Mặt khác, dễ thấy $A_{n}^{1}$ = n. Từ đó suy ra công thức nêu trên.
.png)
Ví dụ 10.
Cho 6 chữ số 2, 3, 4, 5, 6, 7. Hỏi có bao nhiêu số gồm 3 chữ số khác nhau được thành lập từ 6 chữ số này?
Giải.
Số các số gồm 3 chữ số khác nhau lập từ 6 chữ số này là số chỉnh hợp chập 3 của 6, tức là bằng
.png)
Ví dụ 11.
Từ 5 chữ số 0, 1, 3, 5, 7 có thể lập được bao nhiêu số, mỗi số gồm 4 chữ số khác nhau và không chia hết cho 5 ?
Giải.
Số có 4 chữ số khác nhau có dạng: $\overline{a_{1}a_{2}a_{3}a_{4}}$
Có 3 cách chọn $a_{4}$ ($a_{4}$ $\in$ {1,3,7})
Có $A_{4}^{3}$ cách chọn $\overline{a_{1}a_{2}a_{3}}$, kể cả $a_{1}$ = 0.
Với $a_{1}$ = 0, có $A_{3}^{2}$ cách chọn $\overline{a_{2}a_{3}}$.
Vậy có 3($A_{4}^{3}$ - $A_{3}^{2}$) = 54 số thỏa yêu cầu bài toán.
Ví dụ 12.
Với các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số, mỗi số gồm 5 chữ số đôi một khác nhau và trong đó nhất thiết phải có mặt chữ số 5 ?
Giải.
Số có 5 chữ số khác nhau lập được từ các số đã cho là $A_{7}^{5}$ số, kể cả chữ số 0 nằm ở vị trí đầu tiên. Với chữ số 0 nằm ở vị trí đầu tiên có $A_{6}^{4}$ số. Vậy có $A_{7}^{5}$ – $A_{6}^{4}$ số có 5 chữ số khác nhau lập từ các chữ số đã cho.
Tương tự, số có 5 chữ số khác nhau lấy từ các chữ số 0, 1, 2, 3, 4, 6 (trừ số 5 ra) là $A_{6}^{5}$ - $A_{5}^{4}$.
Vậy số các số cần tìm là : $A_{7}^{5}$ - $A_{6}^{4}$ - ($A_{6}^{5}$ - $A_{5}^{4}$) = 1560.
3. Tổ hợp
Cho tập hợp A gồm n phần tử. Mỗi tập hợp con của A gồm k phần tử (0 $\leq$ k $\leq$ n) được gọi là một tổ hợp chập k của n phần tử.
• Công thức tính số tổ hợp chập k của n:
.png)
• Tính chất:
.png)
Ví dụ 13.
Trong 1 bình đựng 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên ra 2 viên. Có bao nhiêu cách lấy được 2 viên cùng màu ?
Giải.
Để hai viên cùng màu đỏ, có .png) cách. Để hai viên cùng màu xanh, có
cách. Để hai viên cùng màu xanh, có .png) cách. Vậy có tất cả 9 cách.
cách. Vậy có tất cả 9 cách.
Ví dụ 14.
Có bao nhiêu số tự nhiên có nhiều nhất là n chữ số (với n > 0) mà tổng các chữ số bằng 3?
Giải.
Số tự nhiên có nhiều nhất n chữ số mà tổng các chữ số bằng 3 có thể là một trong các số:
a) Số chứa 1 chữ số 3, các số còn lại đều là 0. Vì số này có thể có từ 1 đến n chữ số nên có $C_{n}^{1}$ số tự nhiên như thế.
b) Số chứa 1 chữ số 1 và 1 chữ số 2, các số còn lại đều là 0. Có tất cả $A_{n}^{2}$ số tự nhiên như thế.
c) Số chứa 3 chữ số 1, các số còn lại đều là 0. Có tất cả $C_{n}^{3}$ số tự nhiên như thế.
Vậy số các số tự nhiên cần tìm là :
.png)
Ví dụ 15.
a) Có bao nhiêu số chẵn gồm 6 chữ số khác nhau, trong đó, chữ số đầu tiên là chữ số lẻ ?
b) Có bao nhiêu số gồm 6 chữ số khác nhau đôi một, trong đó, có đúng 3 chữ số lẻ và 3 chữ số chẵn (chữ số đầu tiên phải khác không) ?
Giải.
a) Số cần tìm có dạng $\overline{a_{1}a_{2}a_{3}a_{4}a_{5}a_{6}}$, trong đó $a_{6}$ chẵn, $a_{1}$ lẻ. Vậy có 5 cách chọn $a_{1}$, có 5 cách chọn $a_{6}$. Còn lại 8 số xếp vào 4 vị trí còn lại. Vậy có $A_{8}^{4}$ cách chọn 4 vị trí còn lại.
Theo quy tắc nhân ta có
5.5.$A_{8}^{4}$ = 25.5.6.7.8 = 42.000 số.
b) Số cần tìm có dạng $\overline{a_{1}a_{2}a_{3}a_{4}a_{5}a_{6}}$
Bước 1: Chọn $a_{1}$ bất kì.
+ Chọn 3 trong 5 chữ số 0, 2, 4, 6, 8. Do đó có $C_{5}^{3}$ cách chọn 3 chữ số chẵn. Tương tự có $C_{5}^{3}$ cách chọn 3 chữ số lẻ.
+ Xếp 6 chữ số vừa chọn vào 6 vị trí ta có $P_{6}$ = 6! cách.
Theo quy tắc nhân ta có
.png)
Bước 2: Chọn $a_{1}$ = 0.
+ Chọn 2 trong 4 chữ số 2, 4, 6, 8 để có $C_{4}^{2}$ cách chọn 2 chữ số chẵn.
+ Chọn 3 trong 5 chữ số 1, 3, 5, 7, 9 vậy có $C_{5}^{3}$ cách chọn 3 chữ số lẻ.
+ Xếp 5 số vừa tìm được vào 5 vị trí ta có $P_{5}$ = 5! cách.
Theo quy tắc nhân ta có
.png)
Số các số cần tìm bằng số các số tìm ở bước 1, nhưng phải loại đi các số ở bước 2. Vậy có tất cả 72000 - 7200 = 64800 số.
Ví dụ 16.
Có 5 nhà toán học nam, 3 nhà toán học nữ và 4 nhà vật lí nam. Người ta chọn trong số này ra 3 người để lập một đoàn đi công tác, đoàn 3 người này phải thỏa mãn đồng thời hai điều kiện:
(1) Trọng đoàn cần có cả nam lẫn nữ ;
(2) Trong đoàn cần có cả nhà toán học lẫn nhà vật lí.
Hỏi có bao nhiêu cách thành lập đoàn đi công tác ?
Giải.
Để thỏa mãn yêu cầu bài toán, có các trường hợp sau:
Trường hợp 1.
1 nhà toán học nam + 1 nhà toán học nữ + 1 nhà vật lí nam: có 5.3.4 = 60 cách.
Trường hợp 2.
2 nhà toán học nữ + 1 nhà vật lí nam: có $C_{3}^{2}$.4 = 12 cách.
Trường hợp 3.
1 nhà toán học nữ + 2 nhà vật lí nam : có 3.$C_{4}^{2}$ = 18 cách.
Vậy theo quy tắc cộng, ta có 60 + 12 + 18 = 90 cách thỏa mãn yêu cầu bài toán.
Ví dụ 17.
Giải phương trình .png)
Giải.
Để $C_{4}^{x}$ có nghĩa ta phải có 0 $\leq$ x $\leq$ 4. Như vậy x có thể là 0, 1, 2, 3 hay 4. Lần lượt thay các giá trị này vào phương trình, ta được x = 2 là nghiệm,
Ví dụ 18.
Chứng minh rằng: .png)
Giải.
Ta có :
.png)
Cộng vế với vế và rút gọn, ta được :
.png)
Ví dụ 19
Một tập thể nhà khoa học gồm 2 nhà toán học và 10 nhà vật lí. Hỏi có bao nhiêu cách thành lập từ tập thể đó một phái đoàn gồm 8 người trong đó có ít nhất một nhà toán học ?
Giải.
Cách 1. Trong một phái đoàn như thế có thể có 1 nhà toán học và 7 nhà vật lí, hoặc 2 nhà toán học và 6 nhà vật lí. Có $C_{2}^{1}$ = 2 cách chọn 1 nhà toán học và có
.png)
cách chọn 7 nhà vật lí. Theo quy tắc nhân, số cách chọn 1 nhà toán học và 7 nhà vật lí là $C_{7}^{1}$$C_{10}^{7}$ = 2.120 = 240 cách.
Có $C_{2}^{2}$ = 1 cách chọn 2 nhà toán học và có
.png)
cách chọn 6 nhà vật lí. Theo quy tắc nhân, số cách chọn 2 nhà toán học và 6 nhà vật lí là $C_{2}^{2}$$C_{10}^{6}$ = 1.210 = 210 cách.
Vì hai kiểu chọn trên đây khác nhau, nên theo quy tắc cộng, số cách thành lập một phái đoàn trong đó có ít nhất một nhà toán học là 240 + 210 = 450 cách.
Cách 2. Số phái đoàn 8 người có thể lập được từ 12 người là
.png)
Các phái đoàn này có thể chia thành 2 nhóm (1) và (2) không giao nhau.
a) Nhóm (1) gồm các phái đoàn trong đó không có một nhà toán học nào. Nhóm này gồm có .png) phái đoàn.
phái đoàn.
b) Nhóm (2) gồm các phái đoàn trong đó có ít nhất một nhà toán học. Nhóm này gồm có 495 – 45 = 450 phái đoàn.
BÀI TẬP
2.6. Có bao nhiêu cách sắp xếp 6 người vào một bàn tròn có 6 chỗ ngồi ?
2.7. 100000 vé số được đánh số từ 00000 đến 99999. Có bao nhiêu vé có các con số hoàn toàn khác nhau ?
2.8. Tính số chỉnh hợp chập 3 của 5 số 1, 2, 3, 4, 5.
2.9. Có bao nhiêu cách chọn và sắp thứ tự 5 cầu thủ để đá bóng luân lưu 11m, biết rằng cả 11 cầu thủ (kể cả thủ môn) đều có khả năng như nhau ?
2.10. Có 6 thầy giáo tham gia hỏi thi. Mỗi phòng thi cần hai giám khảo. Hỏi có bao nhiêu cách ghép 6 thầy thành đôi để hỏi thi ?
2.11. Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Hỏi có bao nhiêu cách tuyển chọn ?
2.12. Có 20 đội bóng đá tham gia thi đấu tính điểm. Thể lệ cuộc thi là bất kì hai đội nào cũng chỉ gặp nhau một lần. Hỏi phải tổ chức bao nhiêu trận đấu ?
2.13. Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người, biết rằng ban quản trị phải có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn ?
2.14. Có bao nhiêu đường chéo trong một hình thập giác lồi ?
2.15. Có 5 tem thư khác nhau và 6 bì thư khác nhau. Người ta muốn chọn từ đó ra 3 tem thư, 3 bì thư và dán 3 tem thư đó lên 3 bì thư đã chọn, mỗi bì thư chỉ dán 1 tem thư. Hỏi có bao nhiêu cách làm như vậy ?
2.16. Đơn giản các biểu thức
.png)
2.17. Từ 12 người, người ta thành lập một ban kiểm tra gồm 2 người lãnh đạo và 3 uỷ viên. Hỏi có bao nhiêu cách thành lập ban kiểm tra?
2.18. Tính: .png)
2.19. Cho tập hợp A = {1, 2, 3, 4, 5, 6 }. Từ A, lập được bao nhiêu số gồm 3 chữ số đôi một khác nhau và tổng của 3 chữ số này bằng 10?
2.20. Giải các phương trình:
.png)
2.21. Một lớp có 30 học sinh nam, 15 học sinh nữ. Có 6 học sinh được chọn ra để lập nên một đội tốp ca. Hỏi có bao nhiêu cách chọn khác nhau:
a) Nếu phải có ít nhất 2 nữ ?
b) Nếu chọn tuỳ ý ?
HƯỚNG DẪN GIẢI
2.6. Số cách sắp xếp là số hoán vị của 6 phần tử: $P_{n}$ = 6! =120.
2.7. Số vé có các con số hoàn toàn khác nhau là số chỉnh hợp chập 5 của 10 chữ số (0; 1; 2; 3; 4; 5; 6; 7; 8; 9):
$A_{10}^{5}$ = 10.9.8.7.6 = 30240.
2.8. Ta có : $A_{5}^{3}$ = 5.(5 – 1).(5 – 3 + 1) = 5.4.3 = 60.
2.9. Mỗi cách chọn và sắp thứ tự là một chỉnh hợp chập 5 của 11. Do đó số khả năng chọn là
$A_{11}^{5}$ = 11.10.9.8.7 = 55440.
2.10. ĐS: $C_{6}^{2}$ = 15.
2.11. Số cách tuyển chọn là số tổ hợp chập 4 của 9 phần tử :
.png)
2.12. Số trận đấu là : .png)
2.13. Số ban quản trị có thể có là m = 5 . 4 . $C_{7}^{2}$ = 420.
2.14. Một thập giác có 10 đỉnh. Qua mỗi cặp đỉnh có một và chỉ một đường thẳng. Mỗi đoạn thẳng nối cặp điểm đó có thể là đường chéo hoặc là cạnh của hình thập giác lồi. Do đó số đường chéo là :
.png)
2.15.
Để chọn 3 tem thư, có .png) cách. Để chọn 3 bì thư, có
cách. Để chọn 3 bì thư, có .png) cách. Vậy có tất cả 20.10 = 200 cách.
cách. Vậy có tất cả 20.10 = 200 cách.
2.16. a) Ta có :
.png)
b) ĐS: 20.
2.17. Để chọn 2 người lãnh đạo, có $C_{12}^{2}$ cách. Còn lại 10 người để chọn ra 3 ủy viên, do đó có $C_{10}^{3}$ cách. Như vậy, theo quy tắc nhân, có tất cả $C_{12}^{2}$.$C_{10}^{3}$ cách.
2.18. ĐS: -165 . HD : Áp dụng công thức .png)
2.19. Ta có 1 + 3 + 6 = 10 và 2 + 3 + 5 = 10. Do đó số tất cả các số gồm 3 chữ số đôi một khác nhau và tổng của 3 chữ số này bằng 10 là
3! + 3! = 12.
2.20. a) Để (m - 1)! có nghĩa phải có m $\geq$ 1. Khi đó :
.png)
b) ĐS: x = 2;
c) ĐS: x = 1 hoặc x = 2.
2.21. a) Có các trường hợp:
• 2 nữ + 4 nam : có $C_{15}^{2}$$C_{30}^{4}$ cách.
• 3 nữ + 3 nam: có $C_{15}^{3}C_{30}^{3}$ cách.
• 4 nữ + 2 nam : có $C_{15}^{4}C_{30}^{2}$ cách.
• 5 nữ + 1 nam : có $C_{15}^{5}C_{30}^{1}$ cách.
• 6 nữ : có $C_{15}^{6}$ cách.
Vậy theo quy tắc cộng ta có:
$C_{15}^{2}$$C_{30}^{4}$ + $C_{15}^{3}C_{30}^{3}$ + có $C_{15}^{4}C_{30}^{2}$ + $C_{15}^{5}C_{30}^{1}$ + $C_{15}^{6}$ cách.
b) Nếu chọn tuỳ ý, ta có $C_{45}^{6}$ cách.
