§2. VẤN ĐỀ TIẾP TUYẾN CỦA ĐƯỜNG CONG
Trong phần trước, ta đã biết ý nghĩa của đạo hàm : Hệ số góc của tiếp tuyến với đường cong tại một điểm thì bằng đạo hàm của hàm số tại điểm đó. Điều này dẫn đến nhiều dạng bài toán ứng dụng và thường xuất hiện trong các bài toán thi vào đại học.
• Trong phần trước ta cũng có kết quả : Tiếp tuyến tại một điểm ($x_{0}$, $y_{0}$) trên đường cong (C): y = f(x) có phương trình
y = f'($x_{0}$).(x - $x_{0}$) + f($x_{0}$).
• Muốn xác định phương trình tiếp tuyến của đường cong (C) mà tiếp tuyến đó đi qua một điểm $M_{1}$($x_{1}$, $y_{1}$) không nằm trên (C), ta thường tiến hành như sau : Gọi tiếp điểm là $M_{0}$($x_{0}$, f($x_{0}$)) thì phương trình của tiếp tuyến phải tìm là
y = f'($x_{0}$).(x - $x_{0}$) + f($x_{0}$).
Vì tiếp tuyến đó đi qua điểm $M_{1}$($x_{1}$, $y_{1}$) cho trước nên $x_{0}$ là nghiệm của phương trình:
$y_{1}$ = f'($x_{0}$).($x_{1}$ - $x_{0}$) + f($x_{0}$).
• Trong một số trường hợp ta sử dụng điều kiện tiếp xúc của hai đường cong y = f(x), y = g(x) : Phương trình hoành độ giao điểm của hai đường cong là f(x) = g(x), điều kiện tiếp xúc là phương trình này có nghiệm kép.
Ví dụ 23.
Chứng minh rằng trong số các tiếp tuyến của đồ thị hàm số bậc ba y = f(x) = a$x^{3}$ + b$x^{2}$ + cx +d, với a > 0, tiếp tuyến tại điểm $x_{0}$ sao cho f”($x_{0}$) = 0 là tiếp tuyến có hệ số góc nhỏ nhất.
Giải.
.png)
Hệ số góc của tiếp tuyến tại điểm $x_{0}$ này là
.png)
Hệ số góc của tiếp tuyến tại điểm x bất kì là
f'(x) = 3a$x^{2}$ + 2bx + c .
Như vậy, ta cần chứng minh rằng với mọi x, ta phải có
.png)
Ví dụ 24. (Trích đề thi vào ĐH Cần Thơ, 1998)
Cho hàm số y = $x^{3}$ – 3$x^{2}$ + 2 có đồ thị (C). Viết phương trình tiếp tuyến của (C) đi qua điểm A(-1,-2).
Giải.
Gọi tiếp điểm là $M_{0}$($x_{0}$, $y_{0}$) với $y_{0}$ = $x_{0}^{3}$ - 3$x_{0}^{2}$ + 2 thì phương trình tiếp tuyến là
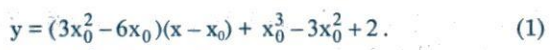
Tiếp tuyến đi qua điểm A(-1, -2), suy ra
.png)
Phương trình có 2 nghiệm $x_{0}$ = -1 và $x_{0}$ = 2. Thế vào (1) ta có 2 tiếp tuyến với phương trình là y = 9x + 7 và y = - 2.
Ví dụ 25.
Cho hàm số y = $x^{3}$ – 3$x^{2}$ + 4 có đồ thị (C). Viết phương trình đường thẳng (d) đi qua điểm A(-1, 0) và có hệ số góc k. Tìm các giá trị của k để (C) tiếp xúc với (d).
Giải.
Ta có y' = 3$x^{2}$ – 6x. Phương trình đường thẳng (d):
y = k(x + 1).
(d) tiếp xúc với (C) ⇔ Tồn tại điểm M($x_{0}$, $y_{0}$)
Thỏa mãn hệ điều kiện sau:
.png)
(Điểm M($x_{0}$, $y_{0}$) chính là tiếp điểm của (d) và (C)).
Thay (2) lên (1) và rút gọn ta được :
$x^{3}$ - 3x - 2 = 0 ⇔ $x_{0}$ = -1, $x_{0}$ = 2
• $x_{0}$ = -1 ⇒ k = 9
• $x_{0}$ = 2 ⇒ k = 0
Vậy (d) tiếp xúc với (C) khi k = 0 hoặc k = 9.
Ví dụ 26.
Cho điểm A($x_{0}$, $y_{0}$) thuộc đồ thị (C) của hàm số
y = $x^{3}$ - 3x + 1.
Tiếp tuyến với (C) tại A cắt (C) tại điểm B khác A. Tìm hoành độ điểm B theo $x_{0}$
Giải.
Miền xác định của hàm số:D = R. Ta có: y' = 3$x^{2}$ - 3.
Phương trình tiếp tuyến tại A:
.png)
Phương trình hoành độ giao điểm của (D) và (C) là:
.png)
Phương trình bậc hai .png)
cho ta hai nghiệm $x_{0}$ và -2$x_{0}$
Vậy B có hoành độ là -2$x_{0}$.
Ví dụ 27. Hãy tìm phương trình của tất cả các tiếp tuyến với đồ thị của hàm số .png)
biết rằng mỗi một trong các tiếp tuyến đó cùng với các trục toạ độ giới hạn một tam giác có diện tích bằng $\large \frac{1}{2}$.
Giải.
Hàm số đã cho có miền xác định là D = R\{0}.
Ta có .png)
Giả sử A(a,f(a)) là điểm nằm trên đồ thị thỏa mãn điều kiện để bài. Tiếp tuyến (D) tại A có phương trình là:
.png)
Từ phương trình này, ta tìm được hai giao điểm B và C của (D) với hai trục tọa độ là:
.png)
Diện tích tam giác OBC là
.png)
Theo đề bài, .png)
hay
.png)
Phương trình (2) vô nghiệm, còn phương trình (1) cho ta
a = 1, a = $\sqrt[3]{5}$.
Tóm lại, có hai tiếp tuyến thỏa mãn đề bài, đó là :
• Tiếp tuyến tại điểm (1,2), có phương trình y = x + 1.
• Tiếp tuyến tại điểm .png)
có phương trình:
.png)
Ví dụ 28. (Trích đề thi vào đại học khối D, 2005)
Cho hàm số: .png)
(m là tham số). Tìm m để đồ thị của hàm số (1) tiếp xúc với đường thẳng y = x.
Giải.
Kí hiệu : .png)
Yêu cầu bài toán tương đương với tìm m để hệ phương trình sau có nghiệm :
.png)
Ta có:
.png)
Ta thấy với mọi m $\neq$ 1, x = m luôn thỏa mãn hệ (*). Vì vậy với mọi m $\neq$ 1, (*) luôn có nghiệm, đồng thời khi m = 1 thì hệ (*) vô nghiệm. Do đó đồ thị hàm số (*) tiếp xúc với đường thẳng y = x khi và chỉ khi m $\neq$ 1.
Ví dụ 29.
Trên đồ thị của hàm số y = $x^{2}$ lấy hai điểm A, B có hoành độ là a, b (a < b). Hãy tìm điểm C trên cung AB mà tiếp tuyến tại đó song song với đường thẳng AB.
Giải.
Hệ số góc của đường thẳng AB là .png)
Do đó, hoành độ của C phải thỏa mãn
.png)
Phương trình tiếp tuyến tại C là
.png)
Ví dụ 30.
Cho hàm số .png)
Xác định m để đồ thị cắt trục hoành tại hai điểm phân biệt và tiếp tuyến tại hai điểm đó vuông góc với nhau.
Giải.
Vì phương trình $x^{2}$ + mx - 8 = 0 (*) có $\Delta$ = $m^{2}$ + 8 > 0 nên đồ thị cắt trục hoành tại hai điểm phân biệt với mọi m. Ta có :
.png)
Nếu đồ thị cắt trục hoành tại x = $x_{0}$ thì u($x_{0}$) = 0, do đó, hệ số góc tiếp tuyến tại điểm này là
.png)
Giả sử đồ thị hàm số cắt trục hoành tại $x_{1}$, $x_{2}$. Hệ số góc tương ứng là .png)
Để hai tiếp tuyến vuông góc với nhau, ta phải có
.png)
Theo định lí Viet ở phương trình (*): $x_{1}$ + $x_{2}$ = -m và $x_{1}$$x_{2}$ = -8, ta có phương trình:
.png)
Vậy, để đồ thị cắt trục hoành tại hai điểm phân biệt và tiếp tuyến tại hai điểm đó vuông góc với nhau, ta phải có
.png)