Chủ đề 1. CĂN BẬC HAI. CĂN BẬC BA

VẤN ĐỀ 1. CĂN BẬC HAI

A. TÓM TẮT LÝ THUYẾT

• Căn bậc hai của số thực a không âm là số thực x sao cho $x^{2}$ = a.

* Chú ý:

+ Số dương a có đúng hai căn bậc hai, là hai số đối nhau:

- Số dương kí hiệu là $\sqrt{a}$

- Số âm kí hiệu là -$\sqrt{a}$

+ Căn bậc hai của số 0 là 0.

+ Số âm không có căn bậc hai.

• Với số a không âm, số $\sqrt{a}$ được gọi là căn bậc hai số học của a.

• Ta có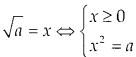

• So sánh hai căn bậc hai số học: $\sqrt{a}$ < $\sqrt{b}$ ⇔ $0\leq a< b$.

B. BÀI TẬP VÀ CÁC DẠNG TOÁN

Dạng 1. Tìm căn bậc hai và căn bậc hai số học của một số

Phương pháp giải: Ta sử dụng kiến thức sau:

1. Nếu a là số thực dương, các căn bậc hai của a là $\sqrt{a}$ và -$\sqrt{a}$; căn bậc hai số học của a là $\sqrt{a}$.

2. Nếu a là số 0 thì căn bậc hai của a và căn bậc hai số học của a cùng bằng 0.

3. Nếu a là số thực âm thì a không có căn bậc hai và do đó không có căn bậc hai số học.

* Giáo viên hướng dẫn học sinh giải các bài tập sau:

Bài 1. Tìm các căn bậc hai và căn bậc hai số học của các số sau:

a) 0; b) 64; c) $\frac{9}{16}$; d) 0,04.

Bài 2. Mỗi số sau đây là căn bậc hai số học của số nào?

a) 12; b) -0,36; c) $2\sqrt{\frac{2}{7}}$; d) $\frac{0,2}{\sqrt{3}}$.

Bài 3. Tính:

a) $\sqrt{9}$; b) $\sqrt{\frac{4}{25}}$; c) $-\sqrt{3^{2}}$;

d) $-\sqrt{(-6)^{2}}$; e) $-(\sqrt{\frac{3}{4}})^{2}$; g) $(-\sqrt{7})^{2}$

Bài 4. Tính giá trị của các biểu thức sau:

a) $\frac{2}{3}\sqrt{81}-\frac{1}{2}\sqrt{16}$;

b) $0,5\sqrt{0,04}+5\sqrt{0,36}$;

c) $\frac{2}{5}\sqrt{\frac{25}{16}}-\frac{1}{2}\sqrt{\frac{4}{9}}$;

d) $-4\sqrt{\frac{-25}{-16}}+5\sqrt{-\frac{-9}{25}}$.

Bài 5. Tìm giá trị của x, biết:

a) $x^{2}$ - 16 = 0; b) $x^{2}$ = 13; c) $x^{2}$ + 9 = 0;

d) $\sqrt{x}$ = 5; k) $-\frac{\sqrt{x}}{3}+2=0$; n) $\sqrt{x^{2}-2x+1}=4$.

* Học sinh tự luyện các bài tập sau tại lớp:

Bài 6. Tìm các căn bậc hai và căn bậc hai số học của các số sau:

a) 81; b) 0,25; c) 1,44; d) $1\frac{40}{81}$.

Bài 7. Mỗi số sau đây là căn bậc hai số học của số nào?

a) 13; b) $-\frac{3}{4}$; c) $\frac{1}{2}\sqrt{\frac{2}{5}}$; d) $\frac{0,12}{\sqrt{0,3}}$.

Bài 8. Tính:

a) $\sqrt{121}$; b) $\sqrt{\frac{16}{25}}$; c) $-\sqrt{(-8)^{2}}$;

d) $(-\sqrt{2})^{2}$; e) $-(\sqrt{\frac{1}{4}})^{2}$; g) $\sqrt{(\frac{3}{5})^{2}}$.

Bài 9. Tính giá trị của các biểu thức sau:

Bài 10. Tìm giá trị của x, biết:

Dạng 2. So sánh các căn bậc hai số học

Phương pháp giải: Ta có $\sqrt{a}$ < $\sqrt{b}$ ⇔ $0\leq a< b$.

* Giáo viên hướng dẫn học sinh giải các bài tập sau:

Bài 11. So sánh:

a) −2 và $\sqrt{3}$; b) 3 và $2\sqrt{2}$; c) 11 và $\sqrt{99}$;

d) 5 và $\sqrt{17}$ + 1; e) 3 và $\sqrt{15}$ – 1; g) 1 - $\sqrt{3}$ và $\sqrt{0,2}$.

Bài 12. Tìm giá trị của x, biết:

Bài 13. Tìm giá trị của x, biết:

* Học sinh tự luyện các bài tập sau tại lớp:

Bài 14. So sánh:

a) 2 và 1 + $\sqrt{2}$; b) 3$\sqrt{11}$ và 12; c) 1 và $\sqrt{3}$ - 1;

d) $\sqrt{3}$ và 2 - $\sqrt{5}$; e) -10 và -2$\sqrt{23}$; g) -3$\sqrt{29}$ và -15.

Bài 15. Tìm giá trị của x, biết:

C. BÀI TẬP VỀ NHÀ

Bài 16. Tìm các căn bậc hai và căn bậc hai số học của các số sau:

a) 225; b) 324; c) $\frac{169}{100}$;

d) $\frac{49}{289}$; e) 2,25; g) 0,16.

Bài 17. Mỗi số sau đây là căn bậc hai số học của số nào?

Bài 18. Tính:

Bài 19. Tính giá trị của các biểu thức sau:

Bài 20. Tìm giá trị của x, biết:

Bài 21. Tìm giá trị của x, biết:

Bài 22. Tìm giá trị của x, biết:

Bài 23. So sánh các số sau:

a) 4 và 1 + $\sqrt{7}$; b) $2\sqrt{5}$ và 8; c) -6 và $-2\sqrt{7}$;

d) 4 và $\sqrt{23}$ - 1; e) $\sqrt{0,5}$ và $\sqrt{3}$ - 2;

g) $\sqrt{2015}$ + $\sqrt{2018}$ và $\sqrt{2016}$ + $\sqrt{2017}$.

Bài 24*. Chứng minh $\sqrt{3}$ và $\sqrt{7}$ là các số vô tỉ.

Bài 25*. Cho biểu thức A = x - 2$\sqrt{x+2}$

a) Đặt y = $\sqrt{x+2}$. Hãy biểu thị A theo y

b) Tìm giá trị nhỏ nhất của A.

Bài 26*. So sánh:

HƯỚNG DẪN – ĐÁP SỐ

Bài 1. Căn bậc hai của các số đã cho lần lượt là:

Căn bậc hai số học của các số đã cho lần lượt là: 0; 8; $\frac{3}{4}$; 0,2.

Bài 2. a) 144; b) Không tồn tại;

c) $\frac{8}{7}$; d) $\frac{1}{75}$.

Bài 3. a) 3; b) $\frac{2}{5}$; c) -3;

d) -6; e) $-\frac{3}{4}$; g) 7.

Bài 4. a) 4; b) 3,1; c) $\frac{1}{6}$; d) -2.

Bài 5. a)

c) Không có giá trị nào của x;

d) x = 25; e) x = 36; g) x = −3 hoặc x = 5.

Bài 6. Căn bậc hai của các số đã cho lần lượt là:

Căn bậc hai số học của các số đã cho lần lượt là:

9; 0,5; 1,2; $\frac{11}{9}$.

Bài 7. a) 169; b) Không tồn tại;

c) $\frac{1}{10}$; d) $\frac{6}{125}$

Bài 8. a) 11; b) $\frac{4}{5}$; c) -8; d)2; e) $-\frac{1}{4}$; g) $\frac{3}{5}$.

Bài 9. a) 1; b) 4,65; c) $-\frac{2}{3}$; d) 6.

Bài 10.

c) x = $\frac{256}{9}$; d) Không có giá trị nào của x;

e) x = 17; g) x = 6 hoặc x = −2.

Bài 11.

Bài 12.

Bài 13.

a) ⇔ 2x $\geq$ x $\geq$ 0 ⇔ x $\geq$ 0;

b) ⇔ 0 $\leq$ 2x $\leq$ $x^{2}$ ⇔ x = 0 hoặc x $\geq$ 2

Bài 14.

a) 2 < 1 + $\sqrt{2}$; b) 3$\sqrt{11}$ < 12;

c) 1 > $\sqrt{3}$ - 1; d) $\sqrt{3}$ > 2 - $\sqrt{5}$;

e) -10 < -2$\sqrt{23}$;

g) -3$\sqrt{29}$ < -15.

Bài 15.

Bài 16. Căn bậc hai của các số đã cho lần lượt là:

Căn bậc hai số học của các số đã cho lần lượt là:

15; 18; $\frac{13}{10}$; $\frac{7}{17}$; 1,5; 0,4.

Bài 17.

a) 49; b) $\frac{9}{16}$; c) $\frac{3}{2}$; d) $\frac{1}{8}$.

Bài 18. a) 5; b) $\frac{7}{5}$ c) -111; d) 13; e) 7; g) $-\frac{1}{400}$.

Bài 19. a) 12; b) $-\frac{7}{20}$; c) $-\frac{11}{4}$; d) $-\frac{13}{4}$.

Bài 20.

d) Không có giá trị nào của x;

e) x = 7; g) x = $\frac{100}{9}$.

Bài 21. a) x = $\frac{290}{3}$; b) x = $\frac{19}{3}$ hoặc x = $-\frac{17}{3}$;

c) Không có giá trị nào của x;

d) x = $\frac{9}{4}$; e) x = 16; g) x = $\frac{13}{4}$.

Bài 22.

c) x $\geq$ 22; d) Không có giá trị nào của x.

Bài 23.

a) 4 > 1 + $\sqrt{7}$; b) 2$\sqrt{5}$ < 8;

c) −6 < −2$\sqrt{7}$; d) 4 > $\sqrt{23}$ − 1;

e) $\sqrt{0,5}$ > $\sqrt{3}$ − 2;

g) So sánh: $(\sqrt{2015}+\sqrt{2018})^{2}$ và $(\sqrt{2016}+\sqrt{2017})^{2}$

Từ đó quy về so sánh:

Bài 24.

* Chứng minh tương tự ta được $\sqrt{7}$ là số vô tỷ.

Bài 25.

a) Đặt y = $\sqrt{x+2}$

⇒ $y^{2}$ = x + 2 ⇒ x = $y^{2}$ - 2

⇒ A = $y^{2}$ - 2y - 2;

b) Ta có:

Từ đó tìm được: $A_{min}$ = -3 tại y = 1 hay x = -1.

Bài 26. a) Ta có: