VẤN ĐỀ 4. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN I)
A. TÓM TẮT LÝ THUYẾT
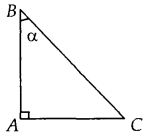
• Cho góc nhọn $\alpha$ (0° < $\alpha$ < 90°). Dựng tam giác ABC vuông tại A sao cho $\alpha$ = $\small \widehat{ABC}$. Từ đó ta có:
.png)
• Với góc góc nhọn $\alpha$ bất kỳ, ta luôn có:
0 < sin $\alpha$ < 1; 0 < cos $\alpha$ < 1.
.png)
.png)
• Nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
• Bảng tỉ số lượng giác của các góc đặc biệt:
.png)
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
Phương pháp giải: Sử dụng các kiến thức trong phần Tóm tắt lý thuyết ở trên.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Cho tam giác ABC vuông tại C có BC = 1,2 cm, AC = 0,9 cm. Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc A.
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Hãy tính sin B và sin C trong các trường hợp sau (làm tròn kết quả đến chữ số thập phân thứ 4):
a) AB = 13 cm, BH = 0,5 dm;
b) BH = 3 cm, CH = 4 cm.
Bài 3. Cho tam giác ABC có AB = a$\sqrt{5}$; BC = a$\sqrt{3}$; AC = a$\sqrt{2}$.
a) Chứng minh ABC là tam giác vuông.
b) Tính các tỉ số lượng giác của góc B. Từ đó suy ra các tỉ số lượng giác của góc A.
Bài 4. Cho tam giác ABC vuông tại A. Hãy tính các tỉ số lượng giác của góc C biết rằng cos B = 0,6.
Bài 5. Cho tam giác ABC vuông tại A, AB = 5 cm, cot B = $\large \frac{5}{8}$. Tính độ dài các đoạn thẳng AC và BC.
* Học sinh tự luyện các bài tập sau tại lớp:
Bài 6. Cho tam giác ABC vuông tại A có BA = 1,6 cm; CA = 1,2cm . Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc C.
Bài 7. Cho ABC có CB = a$\sqrt{5}$; BA = a$\sqrt{3}$; AC = a$\sqrt{2}$.
a) Chứng minh ABC là tam giác vuông.
b) Tính các tỉ số lượng giác của góc B. Suy ra các tỉ số lượng giác của góc C.
Bài 8. Cho tam giác ABC vuông tại A. Cho biết cos B = 0,8. Hãy tính các tỉ số lượng giác của góc C.
Bài 9. Cho tam giác ABC vuông tại A, AB = 6cm, tan B = $\large \frac{5}{12}$. Hãy tính độ dài các cạnh AC và BC.
C. BÀI TẬP VỀ NHÀ
Bài 10. Cho tam giác ABC vuông tại A có AB = 60 mm; AC = 8 cm. Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc C.
Bài 11. Cho tam giác ABC vuông tại A. Biết AB = 30 cm, $\small \widehat{B}$ = $\alpha$, cot $\alpha$ = $\large \frac{5}{12}$. Tính độ dài các cạnh BC, AC.
Bài 12. Tìm sin $\alpha$, cot $\alpha$, tan $\alpha$ biết cos $\alpha$ = $\large \frac{1}{5}$.
Bài 13. Cho tam giác ABC vuông tại A. Tính AC, BC biết:
a) AB = 12cm, tan B = $\large \frac{3}{4}$;
b) AB = 15cm, cos B = $\large \frac{5}{13}$.
Bài 14. Cho tam giác ABC vuông ở A, $\small \widehat{C}$ = 30°, BC = 10 cm.
a) Tính AB, AC.
b) Kẻ từ A các đường thẳng AM, AN lần lượt vuông góc với các đường phân giác trong và ngoài của góc B. Chứng minh MN song song với BC và MN = BC.
c) Chứng minh các tam giác MAB và ABC đồng dạng. Tìm tỉ số đồng dạng.
HƯỚNG DẪN - ĐÁP SỐ
Bài 1.
sin B = $\large \frac{3}{5}$; OK = $\sqrt{41}$; OH = 3.
Bài 2.
a) .png)
.png)
b) .png)
.png)
Bài 3.
a) Vì OK = 2$\sqrt{2}$.
b) sin B = cos A = $\large \frac{\sqrt{10}}{5}$;
cos B = sin A = $\large \frac{\sqrt{15}}{5}$;
tan B = cot A = $\large \frac{\sqrt{6}}{3}$;
cot B = tan A = $\large \frac{3}{\sqrt{6}}$.
Bài 4.
cos C = 0,8; sin C = 0,6;
cot C = $\large \frac{4}{3}$; tan C = $\large \frac{3}{4}$.
Bài 5.
AC = 8; BC = $\sqrt{89}$.
Bài 6.
sin B = cos C = $\large \frac{3}{5}$;
cos B = sin C = $\large \frac{4}{5}$;
tan B = cot C = $\large \frac{3}{4}$;
cot B = tan C = $\large \frac{4}{3}$.
Bài 7.
a) Vì HN = $\large \frac{18\sqrt{13}}{13}$
b) sin B = cos C = $\large \frac{\sqrt{10}}{5}$;
cos B = sin C = $\large \frac{\sqrt{15}}{5}$;
tan B = cot C = $\large \frac{\sqrt{6}}{3}$;
cot B = tan C = $\large \frac{3}{\sqrt{6}}$.
Bài 8.
sin C = 0,8; cos C = 0,6;
cot C = $\large \frac{3}{4}$; tan C = $\large \frac{4}{3}$.
Bài 9.
AC = $\large \frac{5}{2}$; BC = $\large \frac{13}{2}$.
Bài 10.
O $\small \in$ Ay.
Bài 11.
AC = 72; BC = 12$\sqrt{61}$.
Bài 12.
sin $\alpha$ = $\large \frac{2\sqrt{6}}{5}$; tan $\alpha$ = 2$\sqrt{6}$; cot $\alpha$ = $\large \frac{\sqrt{6}}{12}$.
Bài 13.
a) AC = 9; BC = 15.
b) AC = 9$\sqrt{17}$; BC = 39.
Bài 14.
a) AB = 5$\sqrt{3}$; AC = 5.
b) ANBM là hình chữ nhật vì AN // BM, AN = BM;
c) $\Delta$MAB .png) $\Delta$ACB (g-g).
$\Delta$ACB (g-g).
