ÔN TẬP CHỦ ĐỀ 3: HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
A. TÓM TẮT LÝ THUYẾT
1. Hệ thức về cạnh và đường cao trong tam giác vuông
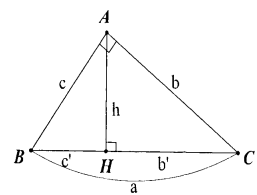
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
• $\small AB^{2}$ = BH.BC hay $c^{2}$ = ac'
• $\small AC^{2}$ = CH.BC hay $b^{2}$ = ab'
• AB. AC = BC. AH hay cb = ah
• $\small HA^{2}$ = HB.HC hay $h^{2}$ = c'b'
.png)
• $\small BC^{2}$ = $\small AB^{2}$ + $\small AC^{2}$ (Định lí Pitago)
2. Tỉ số lượng giác của góc nhọn
• Cho góc nhọn $\alpha$ (0° < $\alpha$ < 90°). Dụng tam giác vuông BAC sao cho $\alpha$ = $\small \widehat{ABC}$. Từ đó ta có:
.png)
• Với góc nhọn $\alpha$ bất kỳ, ta luôn có:
0 < sin $\alpha$ < 1; 0 < cos $\alpha$ < 1.
.png)
• Nếu hai góc phụ nhau thì sin góc này bằng cos góc kia, tan góc này bằng cot góc kia.
• Bảng tỉ số lượng giác của các góc đặc biệt:
.png)
3. Hệ thức về cạnh và góc trong tam giác vuông
• Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Ta có:
b = a.sin B = a.cos C;
c = a.sin C = a.cos B;
b = c.tan B = c.cot C;
c = b.tan C = b.cot B.
• Trong một tam giác vuông
Cạnh góc vuông = (cạnh huyền) x (sin góc đối) = (cạnh huyền) x (cos góc kề)
Cạnh góc vuông = (cạnh góc vuông) x (tan góc đối) = (cạnh góc vuông còn lại) x (cot góc kề)
B. BÀI TẬP TỰ LUYỆN
Bài 1. Cho tam giác ABC vuông tại A, đường cao AH. Trong các đoạn thẳng AB, AC, BC, AH, HB, HC, hãy tính độ dài các đoạn thẳng còn lại nếu biết:
a) AB = 6 cm và AC = 9 cm;
b) AB = 15 cm và HB = 9 cm;
c) AC = 44 cm và BC = 55 cm.
Bài 2. Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH và AH = 12 cm; BC = 25 cm.
a) Tìm độ dài các đoạn thẳng BH, CH, AB và AC.
b) Vẽ trung tuyến AM. Tìm số đo của góc $\small \widehat{AMH}$
c) Tính diện tích tam giác AHM.
Bài 3. Cho tam giác ABC có đường cao CH, BC = 12 cm, $\small \widehat{B}$ = 60° và $\small \widehat{C}$ = 40°.
a) Tính độ dài các đoạn thẳng CH và AC.
b) Tính diện tích tam giác ABC.
Bài 4. Cho tam giác ABC vuông ở A, đường cao AH, AB = 3 cm, AC = 4 cm.
a) Tính độ dài các đoạn thẳng BC và AH;
b) Tính số đo các góc $\small \widehat{B}$ và $\small \widehat{C}$;
c) Đường phân giác trong góc $\small \widehat{A}$ cắt cạnh BC tại E. Tính độ dài các đoạn thẳng BE và CE.
Bài 5. Cho tam giác nhọn ABC có đường cao AH. Từ H kẻ HE vuông góc với AB (E thuộc AB) và kẻ HF vuông góc với AC (F thuộc AC).
a) Chứng minh AE.AB = AF.AC.
b) Cho biết AB = 4 cm, AH = 3 cm. Tính độ dài các đoạn thẳng AE và BE.
c) Cho biết $\small \widehat{HAC}$ = 30°. Tính độ dài đoạn thẳng FC.
Bài 6. Tứ giác MNEF vuông tại M, F, có EF là đáy lớn, hai đường chéo ME và NF vuông góc với nhau tại O.
a) Cho biết MN = 9 cm và MF = 12 cm. Hãy:
i) Giải tam giác MNF;
ii) Tính độ dài các đoạn thẳng MO, FO;
iii) Kẻ NH vuông góc với EF tại H. Tính diện tích tam giác FNE. Từ đó tính diện tích tam giác FOH.
b) Chứng minh $\small MF^{2}$ = MN.FE.
Bài 7. Cho tam giác DEF biết DE = 6 cm, DF = 8 cm, EF = 10 cm.
a) Chứng minh DEF là tam giác vuông.
b) Vẽ đường cao DK. Hãy tính DK, FK.
c) Giải tam giác vuông EDK.
d) Vẽ phân giác trong DM của tam giác DEF. Tính các độ dài các đoạn thẳng ME, MF.
e) Tính sin F trong các tam giác vuông DFK và DEF. Từ đó suy ra ED.DF = DK.EF.
Bài 8. Cho tam giác ABC vuông tại A, $\small \widehat{B}$ = 60° và BC = 6 cm.
a) Tính độ dài các cạnh AB, AC.
b) Trên tia đối của tia BA lấy điểm D sao cho BD = BC. Chứng minh
.png)
c) Đường thẳng song song với phân giác góc $\small \widehat{CBD}$ kẻ từ A cắt CD tại H.
Chứng minh .png)
Bài 9. Cho hình vuông ABCD và điểm E tùy ý trên cạnh BC. Tia Ax vuông góc với AE tại A cắt CD kéo dài tại F. Kẻ trung tuyến AI của tam giác AEF và kéo dài cắt cạnh CD tại K.
a) Chứng minh AE = AF.
b) Chứng minh các tam giác AKF, CAF đồng dạng và $\small AF^{2}$ = KF.CF.
c) Cho AB = 4 cm; BE = $\large \frac{3}{4}$BC . Tính diện tích tam giác AEF.
d) AE kéo dài cắt CD tại J. Chứng minh .png) không phụ thuộc vào vị trí điểm E.
không phụ thuộc vào vị trí điểm E.
Bài 10. Không dùng máy tính, sắp xếp các tỉ số lượng giác sau theo thứ tự từ bé đến lớn:
a) sin24°, cos35°, sin54°, cos70°, sin78°;
b) cot 24°, tan 16°, cot 57°67', cot 30°, tan 80°.
Bài 11. Không dùng máy tính, sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
a) sin 40°, cos 28°, sin 65°, cos 88°, cos 20°;
b) tan 32°48', cot 28°36′, tan 56°32′, cot 67°18′.
Bài 12. Cho $\alpha$ là góc nhọn.
a) Tính sin$\alpha$, cot$\alpha$, tan$\alpha$ biết cos$\alpha$ = $\large \frac{1}{5}$.
b) Tính cos$\alpha$, tan$\alpha$, cot$\alpha$ biết sin$\alpha$ = $\large \frac{2}{3}$.
c) Cho tan$\alpha$ = 2. Tính sin$\alpha$, cos$\alpha$ và cot$\alpha$.
d) Cho cot$\alpha$ = 3. Tính sin$\alpha$, cos$\alpha$ và tan$\alpha$.
Bài 13. Một cột cờ cao 7 m có bóng trên mặt đất dài 4 m. Tính góc $\alpha$ mà tia sáng mặt trời tạo với mặt đất (làm tròn đến phút).
Bài 14. Một cột đèn có bóng trên mặt đất dài 6,5 m, các tia sáng mặt trời tạo với mặt đất một góc xấp xỉ 44°. Tính chiều cao của cột đèn.
Bài 15. a) Tính giá trị biểu thức A = $cos^{2}$20° + $cos^{2}$40° + $cos^{2}$50° + $cos^{2}$70°.
b) Rút gọn biểu thức B = $sin^{6}$$\alpha$ + $cos^{6}$$\alpha$ +3$sin^{2}$$\alpha$ - $cos^{2}$$\alpha$.
Bài 16. Cho 0° < x < 90°. Chứng minh các đẳng thức sau:
a) $sin^{4}$x + $cos^{4}$x = 1 - 2$sin^{2}$x$cos^{2}$x;
b) $sin^{6}$x + $cos^{6}$x = 1 - 3$sin^{2}$x$cos^{2}$x;
c) $sin^{4}$x - $cos^{4}$x = 1 - 2$cos^{2}$x;
Bài 17. Cho 0° < x < 90°. Chứng minh các đẳng thức sau:
.png)
HƯỚNG DẪN - ĐÁP ÁN
Bài 1.
a) BC = 3$\sqrt{13}$cm;
.png)
b) BC = 25 cm; AC = 20 cm; HC = 16 cm; AH = 12 cm.
c) AB = 33cm; AH = $\large \frac{132}{5}$cm; BH = $\large \frac{99}{5}$cm; CH = $\large \frac{176}{5}$cm.
Bài 2.
a) Đặt BH = 9 cm; CH = 16cm; AB = 15 cm; AC = 20 cm.
b) $\small \widehat{AMH}$ ≈ 73,74°.
c) $S_{AHM}$ = 84 $cm^{2}$.
Bài 3.
a) CH = 6$\sqrt{3}$ cm;
.png)
b) .png)
.png)
Bài 4.
a) BC = 5 cm; AH = $\large \frac{12}{5}$ cm;
b) $\small \widehat{B}$ ≈ 53,13°; $\small \widehat{C}$ ≈ 36,87°;
c) BE = $\large \frac{15}{7}$ cm; CE = $\large \frac{20}{7}$ cm.
Bài 5.
a) AE.AB = $\small AH^{2}$ = AE.AC
b) AE = $\large \frac{9}{4}$; BE = $\large \frac{7}{4}$; FC = $\large \frac{\sqrt{3}}{2}$cm.
Bài 6.
a) i) NF = 15cm;
$\small \widehat{MFN}$ ≈ 48,59°; $\small \widehat{MNF}$ ≈ 41,41°.
ii) MO = $\large \frac{36}{5}$; FO = $\large \frac{48}{5}$.
iii) $S_{FNE}$ = 96$cm^{2}$.
.png)
⇒ $S_{FOH}$ = 34,56$cm^{2}$
b) $\Delta$MFN .png) $\Delta$FEM (g-g)
$\Delta$FEM (g-g)
.png)
Bài 7.
a) Vì .png)
b) .png)
c) .png)
.png)
d) .png)
e) .png)
.png)
Bài 8.
a) AB = 3 cm; AC = 6$\sqrt{3}$cm.
b) .png)
.png)
c) .png)
Bài 9.
a) $\Delta$ABE = $\Delta$ADF (g.c.g)
⇒ AE = AF
b) $\small \widehat{F}$ chung, $\small \widehat{FAK}$ = $\small \widehat{FCA}$ = 45°
⇒ $\Delta$AKF .png) $\Delta$CAF (g-g)
$\Delta$CAF (g-g)
.png)
c) $S_{AEF}$ = $\large \frac{93}{2}$$cm^{2}$;
d) .png)
.png)
Bài 10.
a) cos70° (= sin20°) < sin 24° < sin 54° < cos 35° (= sin 55°) < sin 78°;
b) tan 16° (= cot 74°) < cot 57°67' < cot 30° < cot 24° < tan 80° (= cot 10°).
Bài 11.
a) cos 20° < sin 65° (= cos 25°) < cos 28° < sin 40° (= cos 50°) < cos 88°.
b) cot 67°18′(= tan 22°42') < cot 28°36′ (= tan 61°24') < tan 32°48′ < tan 56°32'.
Bài 12.
a) .png)
.png)
b) .png)
.png)
c) .png)
.png)
d) .png)
.png)
Bài 13.
tan $\alpha$ = $\large \frac{7}{4}$ ⇒ $\alpha$ ≈ 60°15'.
Bài 14.
6,28 cm.
Bài 15.
a) A = 2.
b) B = 3$sin^{4}$$\alpha$ + $sin^{2}$$\alpha$.
Bài 16.
a) .png)
.png)
.png)
b) .png)
.png)
.png)
c) .png)
.png)
.png)
Bài 17.
a) .png)
.png)
.png)
b) .png)
.png)
c) Biến đổi tương đương tương tự câu a.
