VẤN ĐỀ 10. LUYỆN TẬP TÍNH CHẤT HAI TIẾP TUYẾN CẮT NHAU
A. TÓM TẮT LÝ THUYẾT
1. Tính chất của hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
• Điểm đó cách đều hai tiếp điểm.
• Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
• Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
2. Đường tròn nội tiếp tam giác
• Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.
• Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong tam giác.
3. Đường tròn bàng tiếp tam giác
• Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với phần kéo dài của hai cạnh còn lại gọi là đường tròn bàng tiếp tam giác.
• Với một tam giác, có ba đường tròn bàng tiếp.
• Tâm của đường tròn bàng tiếp tam giác góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, hoặc là giao điểm của đường phân giác góc A và đường phân giác ngoài tại B (hoặc C).
B. BÀI TẬP TẠI LỚP
* Giáo viên hướng dẫn học sinh giải bài tập sau đây:
Bài 1. Cho nửa đường tròn tâm O đường kính AB = 2R. Kẻ hai tiếp tuyến Ax và By (Ax, By nằm cùng phía đối với nửa đường tròn). Gọi M là một điểm thuộc nửa đường tròn (M khác A và B). Tiếp tuyến tại M với nửa đường tròn cắt Ax và By theo thứ tự ở C và D.
a) Chứng minh $\small \widehat{COD}$ = 90°.
b) Chứng minh bốn điểm B, D, M, O nằm trên một đường tròn. Chỉ ra bán kính của đường tròn đó.
c) Chứng minh CD = AC + BD.
d) Chứng minh tích AC.BD không đổi khi M thay đổi trên (O).
e) Chứng minh AB là tiếp tuyến của đường tròn đường kính CD.
g) Gọi giao điểm AD và BC là N. Chứng minh MN và AC song song.
h) Gọi BN' là tia phân giác của $\small \widehat{ABD}$ (N′ thuộc OD). Chứng minh:
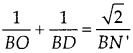
* Học sinh tự luyện các bài tập sau đây tại lớp:
Bài 2. Cho đường tròn (O; R). Từ điểm A nằm ngoài đường tròn kẻ các tiếp tuyến AB, AC với đường tròn ( B, C là các tiếp điểm). Gọi H là trung điểm của BC.
a) Chứng minh ba điểm A, H, O thẳng hàng và các điểm A, B, C, O cùng thuộc một đường tròn.
b) Kẻ đường kính BD của (O). Vẽ CK $\small \perp$ BD. Chứng minh:
AC.CD = CK.AO.
c) Tia AO cắt đường tròn (O) tại M (M nằm giữa A và O). Chứng minh M là tâm đường tròn nội tiếp tam giác ABC.
d) Gọi I là giao điểm của AD và CK. Chứng minh I là trung điểm của CK.
Bài 3. Cho đường tròn (O; R), đường kính AB. Điểm M bất kỳ thuộc (O; R). Tiếp tuyến tại M và B cắt nhau tại D. Qua O kẻ đường thẳng song song với MB cắt tiếp tuyến qua M tại C, cắt tiếp tuyến qua B tại N.
a) Chứng minh rằng tam giác CDN cân;
b) Chứng minh AC là tiếp tuyến của nửa đường tròn (O);
c) Chứng minh AC.BD không phụ thuộc vào M;
d) Gọi H là hình chiếu của M trên AB. Tia phân giác của $\small \widehat{HOM}$ cắt (O) tại K (K khác M). Xác định vị trí điểm M sao cho $\large \frac{MH}{HK}$ = $\large \frac{\sqrt{15}}{5}$.
C. BÀI TẬP VỀ NHÀ
Bài 4. Cho đường tròn (O; 3cm) và điểm A có OA = 6 cm. Kẻ các tiếp tuyến AB và AC với đường tròn (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC.
a) Tính độ dài đoạn thẳng OH.
b) Qua điểm M bất kì thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn, cắt AB và AC theo thứ tự tại E và F. Tính chu vi tam giác ADE.
c) Tính số đo góc $\small \widehat{DOE}$.
Bài 5. Cho tam giác MBC cân tại M. I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp trong góc M. O là trung điểm của IK.
a) Chứng minh bốn điểm B, I, C, K cùng thuộc một đường tròn tâm O;
b) Chứng minh MC là tiếp tuyến của đường tròn (O);
c) Tính bán kính đường tròn (O) biết MB = MC = 10 cm, BC = 12 cm.
HƯỚNG DẪN - ĐÁP SỐ
Bài 1.
a) $\small \widehat{COA}$ = $\small \widehat{COM}$, $\small \widehat{DOM}$ = $\small \widehat{DOB}$
⇒ $\small \widehat{COD}$ = 90°;
b) $\small \widehat{OBD}$ = $\small \widehat{OMD}$ = 90°
⇒ B, D, M, O $\small \in$ đường tròn bán kính $\large \frac{OD}{2}$;
c) CD = MC + MD = AC + BD;
d) AC.BD = MC.MD = $\small MO^{2}$ = $\small R^{2}$;
e) Gọi I là trung điểm của CD ⇒ I là tâm của đường tròn đường kính CD và IO là đường trung bình của hình thang vuông ACDB nên IO $\small \perp$ AB = O;
f) .png)
g) BN' $\small \cap$ OI = {K} ⇒ OB = OK
Ta có:
.png)
.png)
Bài 2.
a) AO là trung trực của BC ⇒ A, H, O thẳng hàng.
$\small \widehat{ABO}$ + $\small \widehat{ACO}$ = 180° ⇒ A, B, C, O nằm trên đường tròn đường kính AO;
b) $\small \widehat{CDK}$ = $\small \widehat{COA}$
⇒ $\small \Delta$ACO ~ $\small \Delta$CKD (g.g)
⇒ AC.CD = CK.AO;
c) AM là phân giác góc A của $\small \Delta$ABC. Chứng minh BM là phân giác góc B của $\small \Delta$ABC
⇒ M là tâm đường tròn nội tiếp $\small \Delta$ABC;
d) Theo câu b):
.png) IK // AB
IK // AB
.png)
.png)
.png)
⇒ I là trung điểm của CK.
Bài 3.
a) Chứng minh DO vừa là phân giác vừa là đường cao của $\small \Delta$CDN ⇒ $\small \Delta$CDN cân tại D;
c) AC.BD = MC.MD = $\small R^{2}$.
Bài 4.
a) OH = 1,5 cm;
b) $P_{ADE}$ = 6$\sqrt{3}$ cm;
c) $\small \widehat{DOE}$ = 60°.
Bài 5.
a) $\small \Delta$ABC có BI, BK lần lượt là phân giác trong và ngoài tại B
⇒ $\small \widehat{IBK}$ = 90° ⇒ B, I, C, K $\small \in$ (O; $\large \frac{IK}{2}$)
Ta có: $\small \widehat{MCI}$ = $\small \widehat{IBC}$ = $\small \widehat{IKC}$ = $\small \widehat{OCK}$
Mặt khác, $\small \widehat{OCK}$ + $\small \widehat{OCI}$ = 90°
⇒ $\small \widehat{MCI}$ + $\small \widehat{OCI}$ = 90°
⇒ OC $\small \perp$ CM
⇒ MC là tiếp tuyến của (O);
c) Gọi D là giao điểm của MO và BC
⇒ CD = $\large \frac{BC}{2}$ = 6 cm
.png)
⇒ OC = 7,5 cm = R.
