VẤN ĐỀ 11. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN
A. TÓM TẮT LÝ THUYẾT
1. Tính chất của đường nối tâm:
Đường nối tâm là trục đối xứng của hình tạo bởi hai đường tròn. Từ đó suy ra:
- Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm
- Nếu hai đường tròn cắt nhau thì đường nối tâm là đường trung trực của dây chung.
2. Sự liên hệ giữa vị trí của hai đường tròn với đoạn nối tâm d và các bán kính R và r
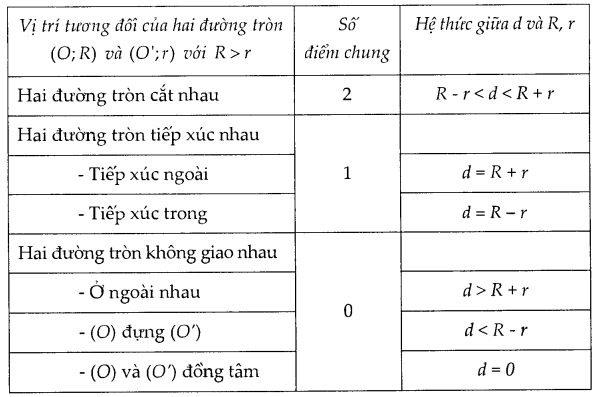
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Các bài toán có cho hai đường tròn tiếp xúc nhau
Phương pháp giải:
- Vẽ đường nối tâm và chú ý rằng tiếp điểm nằm trên đường nối tâm, dùng hệ thức d = R + r.
- Nếu cần, có thể vẽ tiếp tuyến chung tại tiếp điểm
* Giáo viên hướng dẫn học sinh giải bài tập sau:
Bài 1. Cho đường tròn (O) và (O') tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B $\small \in$ (O), C $\small \in$ (O'). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC ở I.
a) Chứng minh $\small \widehat{BAC}$ = 90°.
b) Tính số đo góc OIO'.
c) Tính độ dài BC biết OA = 9 cm; OA' = 4 cm.
* Học sinh tự luyện tập bài sau tại lớp:
Bài 2. Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài với nhau tại A. Vẽ tiếp tuyến chung ngoài BC, B $\small \in$ (O), C $\small \in$ (O’).
a) Chứng minh ABC là tam giác vuông.
b) Tính số đo góc OMO'.
c) Tính diện tích tứ giác BCO’O theo R và r.
d) Gọi I là trung điểm của OO'. Chứng minh rằng BC là tiếp tuyến của đường tròn (I; IM).
Dạng 2. Các bài toán cho hai đường tròn cắt nhau
Phương pháp: Vẽ dây chung của hai đường tròn rồi dùng tính chất đường nối tâm là đường trung trực của dây chung
* Giáo viên hướng dẫn học sinh giải bài toán sau:
Bài 3. Cho hai đường tròn (O) và (O') cắt nhau tại A và B, trong đó OA là tiếp tuyến của đường tròn (O'). Tính độ dài dây cung AB biết OA = 20 cm, O'A = 15 cm.
* Học sinh tự luyện tập các bài sau tại lớp:
Bài 4. Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Từ A vẽ đường kính AOC và AOD. Chứng minh ba điểm B, C, D thẳng hàng và vuông góc với AB.
Bài 5. Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Gọi M là trung điểm của OO'. Qua A kẻ đường thẳng vuông góc với AM, cắt các đường tròn (O) và (O’) ở C và D. Chứng minh rằng AC = AD.
C. BÀI TẬP VỀ NHÀ
Bài 6. Cho hai đường tròn (O; R) và (O'; r) tiếp xúc với nhau tại A. Vẽ một cát tuyến qua A cắt hai đường tròn tại B và C. Chứng minh các tiếp tuyến tại B và C song song với nhau.
Bài 7. Cho góc vuông $\small \widehat{xOy}$. Lấy các điểm I và K thứ tự trên các tia Ox và Oy. Vẽ đường tròn (I; OK) cắt tia Ox tại M (I nằm giữa O và M). Vẽ đường tròn (K; OI) cắt tia Oy tại N (K nằm giữa O và N).
a) Chứng minh hai đường tròn (I) và (K) luôn cắt nhau.
b) Tiếp tuyến tại M của đường tròn (I), tiếp tuyến tại N của (K) cắt nhau tại C. Chứng minh tứ giác OMCN là hình vuông.
c) Gọi giao điểm của hai đường tròn là A và B. Chứng minh ba điểm A, B, C thẳng hàng.
d) Giả sử I và K thứ tự di động trên các tia Ox và Oy sao cho OI + OK = a không đổi. Chứng minh đường thẳng AB luôn đi qua một điểm cố định.
Bài 8. Cho đường tròn (O) và một điểm A trên đường tròn đó. Trên đoạn OA lấy điểm B sao cho OB = $\large \frac{1}{3}$OA . Vẽ đường tròn đường kính AB.
a) Chứng minh đường tròn đường kính AB tiếp xúc với đường tròn (O) cho trước.
b) Vẽ đường tròn đồng tâm (O) với đường tròn (O) cho trước, cắt đường tròn đường kính AB tại C. Tia AC cắt hai đường tròn đồng tâm tại D và E (D nằm giữa C và E). Chứng minh AC = CD = DE.
Bài 9. Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (I) có đường kính CB.
a) Xét vị trí tương đối của hai đường tròn (O) và (I).
b) Kẻ dây DE của đường tròn (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì? Vì sao?
c) Gọi K là giao điểm của DB và đường tròn (I). Chứng minh ba điểm E, C, K thẳng hàng.
d) Chứng minh HK là tiếp tuyến của đường tròn (I).
HƯỚNG DẪN - ĐÁP SỐ
Bài 1.
a) Có: IA = IB = IC nên tam giác ABC vuông tại A;
b) $\small \widehat{OIO'}$ = 90°;
c) BC = 12.
Bài 2.
a) Từ MA = MB = MC ⇒ $\small \Delta$ABC vuông tại A;
b) $\small \widehat{OMO'}$ = 90°;
c) S = (R + r)$\sqrt{Rr}$;
d) OBCO' là hình thang vuông tại B và C có IM là đường trung bình ⇒ IM $\small \perp$ BC = M.
Bài 3
AB = 24 cm.
Bài 4.
Ta có $\small \widehat{ABC}$ + $\small \widehat{ABD}$ = 180°.
Bài 5.
Gọi P, Q lần lượt là trung điểm của AC và AD
⇒ AM là đường trung bình của hình thang OPQO'
⇒ AP = AQ ⇒ AC = AD.
Bài 6.
Ta có: $\small \widehat{OBA}$ = $\small \widehat{OAB}$ = $\small \widehat{O'AC}$ = $\small \widehat{O'CA}$
⇒ OB // O'C ⇒ đpcm.
Bài 7.
a) Ta có: KI < OI + OK
⇒ (I) và (K) luôn cắt nhau;
b) Do OI = NK; OK = IM ⇒ OM = ON.
Mặt khác OMCN là hình chữ nhật ⇒ OMCN là hình vuông;
c) Gọi L = KP $\small \cap$ MC, P = IB $\small \cap$ NC
⇒ OKBI là hình chữ nhật và BLMI là hình vuông
⇒ $\small \Delta$BLC = $\small \Delta$OKI.
⇒ $\small \widehat{LBC}$ = $\small \widehat{OKI}$ = $\small \widehat{BIK}$
Mà: $\small \widehat{BIK}$ + $\small \widehat{IBA}$ = 90°
⇒ $\small \widehat{LBC}$ + $\small \widehat{IBA}$ = 90°
⇒ $\small \widehat{LBC}$ + $\small \widehat{IBA}$ + $\small \widehat{IBL}$ = 180°;
d) Có OMCN là hình vuông cạnh a cố định ⇒ C cố định và AB luôn đi qua C.
Bài 8.
a) Gọi I là trung điểm của AB, ta có: OI = OA - IA;
b) Ta chứng minh được IC // BD // OE. Mà OB = BI = IA
⇒ AC = CD = DE.
Bài 9.
a) (O) và (I) tiếp xúc trong với nhau;
b) ADCE là hình thoi;
c) Có CK $\small \perp$ AB, AD $\small \perp$ DB
⇒ CK // AD mà CE // AD
⇒ B, K, D thẳng hàng;
d) $\small \widehat{HKD}$ = $\small \widehat{HDK}$; $\small \widehat{IKB}$ = $\small \widehat{IBK}$
⇒ $\small \widehat{HKD}$ + $\small \widehat{IKB}$ = $\small \widehat{HDK}$ + $\small \widehat{IBK}$ = 90°
⇒ $\small \widehat{IKH}$ = 90°.
