Đồ thị của hàm số bậc nhất

VẤN ĐỀ 3. ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT

A. TÓM TẮT LÝ THUYẾT

• Đồ thị của hàm số y = ax + b (a ≠ 0) là một đường thẳng.

• Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0):

+ Nếu b = 0 ta có hàm số y = ax. Đồ thị của y = ax là đường thẳng đi qua gốc toạ độ O(0; 0) và điểm A(1;a).

+ Nếu b ≠ 0 thì đồ thị y = ax + b là đường thẳng đi qua các điểm A(0;b), B(-$\large \frac{b}{a}$;0).

B. BÀI TẬP VÀ CÁC DẠNG TOÁN

Dạng 1. Vẽ đồ thị hàm số y = ax + b (a ≠ 0) và tìm tọa độ giao điểm của hai đường thẳng

Phương pháp giải: Ta thường sử dụng các kiến thức sau:

1. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0):

Trường hợp 1. Nếu b = 0 thì đồ thị hàm số là đường thẳng đi qua hai điểm O(0;0) và A(1;a).

Trường hợp 2. Nếu b ≠ 0 thì đồ thị hàm số là đường thẳng đi qua hai điểm A(0;b), B(-$\large \frac{b}{a}$;0).

2. Cách tìm tọa độ giao điểm của hai đường thẳng:

Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.

Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm.

* Giáo viên hướng dẫn học sinh giải các bài tập sau:

Bài 1. Cho ba đường thẳng $d_{1}$: y = 2x - 2, $d_{2}$: y = -$\large \frac{4}{3}$x - 2 và $d_{3}$: y = $\large \frac{1}{3}$x + 3.

a) Vẽ các đường thẳng $d_{1}$, $d_{2}$ và $d_{3}$ trên cùng một mặt phẳng tọa độ.

b) Gọi giao điểm của đường thẳng $d_{3}$ với $d_{1}$ và $d_{2}$ theo thứ tự là A, B. Hãy tìm tọa độ của A, B.

Bài 2. Cho các hàm số y = x + 1 có đồ thị là $d_{1}$ và y = -x + 3 có đồ thị là $d_{2}$.

a) Vẽ đồ thị hai hàm số trên trên cùng một mặt phẳng tọa độ.

b) Gọi A, B lần lượt là giao điểm của $d_{1}$, $d_{2}$ với trục hoành và C là giao điểm của $d_{1}$ và $d_{2}$. Hãy tìm tọa độ các điểm A, B và C.

c) Tính chu vi và diện tích của tam giác ABC.

Học sinh tự luyện các bài tập sau tại lớp:

Bài 3. Cho ba đường thẳng:

$d_{1}$: y = -2x - 2, $d_{2}$: y = -$\large \frac{4}{3}$x - 2 và $d_{3}$: y = -$\large \frac{1}{3}$x + 3.

a) Vẽ các đường thẳng $d_{1}$, $d_{2}$ và $d_{3}$ trên cùng một mặt phẳng tọa độ.

b) Gọi giao điểm của đường thẳng $d_{3}$ với $d_{1}$ và $d_{2}$ theo thứ tự là A, B. Hãy tìm tọa độ của A, B.

Bài 4. Cho hai hàm số y = -x + 1 có đồ thị là $d_{1}$ và y = x + 3 có đồ thị là $d_{2}$.

a) Vẽ đồ thị hai hàm số trên trên cùng một mặt phẳng tọa độ.

b) Hai đường thẳng $d_{1}$ và $d_{2}$ cắt nhau tại C và cắt trục Ox theo thứ tự tại A, B. Tìm tọa độ của các điểm A, B, C.

c) Tính chu vi và diện tích của tam giác ABC.

Dạng 2. Xác định các hệ số a, b để đồ thị hàm số y = ax + b (a ≠ 0) cắt trục Ox, Oy hay đi qua một điểm nào đó

Phương pháp giải: Đồ thị hàm số y = ax + b (a ≠ 0) đi qua điểm M($x_{M}$;$y_{M}$) khi và chỉ khi

$y_{M}$ = a$x_{M}$ + b.

*Giáo viên hướng dẫn học sinh giải các bài tập sau:

Bài 5. Cho hàm số y = (m - 2)x + m.

a) Xác định giá trị của tham số m để đồ thị hàm số:

i) Cắt trục hoành tại điểm có hoành độ bằng -3.

ii) Cắt trục tung tại điểm có tung độ bằng 4.

b) Vẽ đồ thị của hai hàm số ứng với các giá trị của m tìm được ở trên trên cùng hệ trục toạ độ Oxy và tìm tọa độ giao điểm của hai đồ thị vừa vẽ được.

Bài 6. Gọi $d_{1}$ là đồ thị hàm số y = mx + 2 và $d_{2}$ là đồ thị hàm số y = $\large \frac{1}{2}$x - 1.

a) Với m = -$\large \frac{1}{2}$, xác định tọa độ giao điểm của $d_{1}$ và $d_{2}$.

b) Xác định giá trị của m để M(-3;-3) là giao điểm của $d_{1}$ và $d_{2}$.

Bài 7. Với giá trị nào của m thì đồ thị hàm số y = -3x + m + 2 và y = 4x - 5 - 2m cắt nhau tại một điểm trên trục tung?

* Học sinh tự luyện các bài tập sau tại lớp:

Bài 8. Cho hàm số: y = (2 - m)x + m + 1.

a) Xác định giá trị của tham số m để đồ thị hàm số:

i) Cắt trục hoành tại điểm có hoành độ bằng -2.

ii) Cắt trục tung tại điểm có tung độ bằng -4.

b) Vẽ đồ thị của hai hàm số ứng với các giá trị của m tìm được ở trên trên cùng hệ trục tọa độ Oxy và tìm tọa độ giao điểm của hai đồ thị vừa vẽ được.

Bài 9. Gọi $d_{1}$ là đồ thị hàm số y = mx - 2 và $d_{2}$ là đồ thị hàm số y = -$\large \frac{1}{2}$x - 1.

a) Với m = -$\large \frac{1}{3}$, xác định tọa độ giao điểm của $d_{1}$ và $d_{2}$.

b) Xác định giá trị của m để M(-3;-3) là giao điểm của $d_{1}$ và $d_{2}$.

Bài 10. Với giá trị nào của m thì đồ thị hàm số y = -2x + m + 2 và y = 5x - 5 - 2m cắt nhau tại một điểm trên trục tung?

Dạng 3. Xét tính đồng quy của ba đường thẳng

Phương pháp giải: Để xét tính đồng quy của ba đường thẳng cho trước, ta làm như sau:

Bước 1. Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho.

Bước 2. Kiểm tra xem nếu giao điểm vừa tìm được thuộc đường thẳng còn lại thì kết luận ba đường thẳng đó đồng quy.

* Giáo viên hướng dẫn học sinh giải các bài tập sau:

Bài 11. Cho ba đường thẳng $d_{1}$: y = -3x; $d_{2}$: y = 2x + 5; $d_{3}$: y = x + 4.

a) Gọi A là giao điểm của hai đường thẳng $d_{1}$, $d_{2}$. Tìm tọa độ điểm A.

b) Chứng minh ba đường thẳng $d_{1}$, $d_{2}$, $d_{3}$ đồng quy.

Bài 12. Cho ba đường thẳng $d_{1}$: y = 2x, $d_{2}$: y = -x - 3 và $d_{3}$: y = mx + 5.

a) Tìm tọa độ giao điểm của hai đường thẳng $d_{1}$, $d_{2}$.

b) Tìm các giá trị của tham số m để ba đường thẳng $d_{1}$, $d_{2}$, $d_{3}$ đồng quy.

* Học sinh tự luyện các bài tập sau tại lớp:

Bài 13. Cho ba đường thẳng $d_{1}$: y = x - 4; $d_{2}$: y = -2x + 2; $d_{3}$: y = 1,2x - 4,4.

a) Gọi I là giao điểm của hai đường thẳng $d_{1}$, $d_{2}$. Tìm tọa độ điểm I.

b) Chứng minh rằng ba đường thẳng $d_{1}$, $d_{2}$, $d_{3}$ đồng quy.

Bài 14. Cho ba đường thẳng $d_{1}$: y = 2x + 1, $d_{2}$: y = 3x - 1 và $d_{3}$: y = x + 3.

a) Chứng minh ba đường thẳng trên đồng quy.

b) Với giá trị nào của m thì đường thẳng y = (m - 1)x + m cũng đi qua giao điểm của các đường thẳng đó?

C. BÀI TẬP VỀ NHÀ

Bài 15. Cho các hàm số y = x và y = 3x + 3.

a) Vẽ đồ thị các hàm số trên trên cùng một hệ trục tọa độ.

b) Tìm tọa độ giao điểm M của hai đồ thị trên.

Bài 16. Cho ba đường thẳng $d_{1}$: y = x - 2, $d_{2}$: y = -$\large \frac{1}{3}$x - 2 và $d_{3}$: y = $\large \frac{1}{3}$x + 3.

a) Vẽ các đường thẳng $d_{1}$, $d_{2}$ và $d_{3}$ trên cùng một mặt phẳng tọa độ.

b) Gọi giao điểm của đường thẳng $d_{3}$ với $d_{1}$ và $d_{2}$ theo thứ tự là A, B. Hãy tìm tọa độ của A, B.

Bài 17. Cho hàm số y = 2x + 1 có đồ thị là $d_{1}$ và y = -x + 3 có đồ thị là $d_{2}$.

a) Vẽ đồ thị hai hàm số trên trên cùng một mặt phẳng tọa độ.

b) Hai đường thẳng $d_{1}$ và $d_{2}$ cắt nhau tại C và cắt trục Ox theo thứ tự A, B. Tìm tọa độ của các điểm A, B, C.

c) Tính chu vi và diện tích của tam giác ABC.

Bài 18. Cho hàm số: y = (m + 5)x - m.

a) Xác định giá trị của tham số m để đồ thị hàm số:

i) Cắt trục hoành tại điểm có hoành độ bằng 3.

ii) Cắt trục tung tại điểm có tung độ bằng -4.

c) Vẽ đồ thị của hai hàm số ứng với các giá trị của m tìm được ở trên trên cùng hệ trục toạ độ Oxy và tìm tọa độ giao điểm của hai đồ thị vừa vẽ được.

Bài 19. Gọi $d_{1}$ là đồ thị hàm số y = mx + 1 và $d_{2}$ là đồ thị hàm số y = $\large \frac{1}{2}$x - 2.

a) Với m = -$\large \frac{1}{2}$, xác định toạ độ giao điểm của $d_{1}$ và $d_{2}$.

b) Xác định giá trị của m để M(-2;-2) là giao điểm của $d_{1}$ và $d_{2}$.

Bài 20. Với giá trị nào của tham số m thì đồ thị hàm số y = 4x + (m + 2) và y = -2x - 5 - 2m cắt nhau tại một điểm trên trục tung?

Bài 21. Cho ba đường thẳng $d_{1}$: y = -2x, $d_{2}$: y = 1,5x + 7 và $d_{3}$: y = -2mx + 5.

a) Tìm tọa độ giao điểm của hai đường thẳng $d_{1}$, $d_{2}$.

b) Tìm các giá trị của tham số m để ba đường thẳng $d_{1}$, $d_{2}$, $d_{3}$ đồng quy.

Bài 22. Cho ba đường thẳng $d_{1}$: y = -2x, $d_{2}$: y = x - 3 và $d_{3}$: y = mx + 4

a) Tìm tọa độ giao điểm của hai đường thẳng $d_{1}$, $d_{2}$.

b) Tìm các giá trị của tham số m để ba đường thẳng $d_{1}$, $d_{2}$, $d_{3}$ đồng quy.

HƯỚNG DẪN - ĐÁP SỐ

Bài 1.

a) Học sinh tự vẽ;

b) A(3;4), B(-3;2).

Bài 2.

a) Học sinh tự vẽ;

b) A(-1;0), B(3;0), C(1;2);

c) $C_{ABC}$ = 4 + 4$\sqrt{2}$; $S_{ABC}$ = 4.

Bài 3.

a) Học sinh tự vẽ;

b) A(-3;4), B(-5;$\large \frac{14}{3}$).

Bài 4.

a) Học sinh tự vẽ;

b) A(1;0), B(-3;0), C(-1;2);

c) $C_{ABC}$ = 4 + 4$\sqrt{2}$; $S_{ABC}$ = 4.

Bài 5.

a) i) m = 3, ii) m = 4; b) I(-1;2).

Bài 6.

a) I(3;$\large \frac{1}{2}$); b) m $\small \in$ Ø.

Bài 7.

m = -$\large \frac{7}{3}$.

Bài 8.

a) i) m = 1; ii) m = -5; b) I(1;3).

Bài 9.

a) I(6;-4); b) m $\small \in$ Ø.

Bài 10.

m = -$\large \frac{7}{3}$.

Bài 11.

a) A(-1;3);

b) A(-1;3) = $d_{1}$ $\small \cap$ $d_{2}$ $\small \in$ $d_{3}$ ⇒ đpcm.

Bài 12.

a) I(-1;-2); b) m = 7.

Bài 13.

a) I(2;-2); b) I $\small \in$ $d_{3}$.

Bài 14.

a) I(2;5); b) m = $\large \frac{7}{3}$.

Bài 15.

a) Học sinh tự vẽ;

b) M(-$\large \frac{3}{2}$;-$\large \frac{3}{2}$).

Bài 16.

a) Học sinh tự vẽ;

b) A ($\large \frac{15}{2}$;$\large \frac{11}{2}$), B(-$\large \frac{15}{2}$;$\large \frac{1}{2}$).

Bài 17.

a) Học sinh tự vẽ;

b) A(-$\large \frac{1}{2}$;0), B(3;0), C($\large \frac{2}{3}$;$\large \frac{7}{3}$);

c)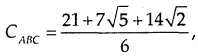

$S_{ABC}$ = $\large \frac{49}{18}$.

Bài 18.

a) i) m = -$\large \frac{15}{2}$, ii) m = 4;

b) (1;5).

Bài 19.

a) I(3;-$\large \frac{1}{2}$); b) m $\small \in$ Ø.

Bài 20.

m = -$\large \frac{7}{3}$.

Bài 21.

a) I(-2;4); b) m = -$\large \frac{1}{4}$.

Bài 22.

a) I(1;-2); b) m = -6.