BÀI TẬP ÔN CHƯƠNG 5
49. Tìm đạo hàm của các hàm số sau :
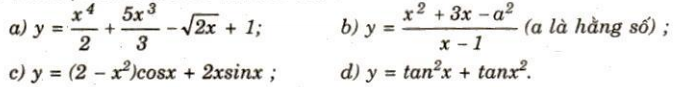
Giải
.png)
50. a) Chứng minh rằng .png)
trong đó n $\in$ N*
b) Hãy so sánh với công thức ($x^{n}$)' = n$x^{n-1}$ và nêu nhận xét.
Giải
a) Ta có .png)
b) Ta có ($x^{-n}$)' = -n$x^{-n-1}$ (Theo a).
Nhận xét : Công thức ($x^{n}$)' = n$x^{n-1}$ đúng với mọi giá trị nguyên của n (chú ý rằng khi n $\leq$ 0 thì chỉ có thể xét đạo hàm trên (-$\infty$; 0) $\cup$ (0; +$\infty$)).
51. Tìm đạo hàm đến cấp được nêu kèm theo của các hàm số sau (n $\in$ N*)
.png)
Giải
.png)
52. Tính vi phân của hàm số .png)
tại điểm .png)
ứng với .png)
(tính chính xác đến hàng phần vạn)
Giải
.png)
53. Gọi (C) là đồ thị của hàm số f(x) = $x^{4}$ + 2$x^{2}$ - 1. Viết phương trình tiếp tuyến của (C) trong mỗi trường hợp sau:
a) Biết tung độ của tiếp điểm bằng 2;
b) Biết rằng tiếp tuyến song song với trục hoành;
c) Biết rằng tiếp tuyến vuông góc với đường thẳng .png)
d) Biết rằng tiếp tuyến đi qua điểm A(0; -6).
Giải
a) f(x) = 4$x^{3}$ + 4x. Ta có 2 = $y_{0}$ = $x_{0}^{4}$ + 2$x_{0}^{2}$ -1 ⇔ $x_{0}^{4}$ + 2$x_{0}^{2}$ - 3 = 0
.png)
* Với $x_{0}$ = 1 ta có f'(1) = 4.$1^{3}$ + 4.1 = 8
Phương trình tiếp tuyến trong trường hợp này là :
y - 2 = 8(x - 1) ⇔ y = 8x - 6
* Với $x_{0}$ = -1 ta có f'(-1) = 4.$(-1)^{3}$ + 4.(-1) = -8
Phương trình tiếp tuyến trong trường hợp này là :
y - 2 = -8(x + 1) ⇔ y = -8x - 6
b) Tiếp tuyến song song với trục hoành tại điểm có hoành độ $x_{0}$ thỏa :
.png)
Phương trình tiếp tuyến cần tìm là :
y = (-1) = 0(x - 0) ⇔ y = - 1
c) Vì tiếp tuyến phải tìm vuông góc với đường thẳng .png)
nên hệ số góc của tiếp tuyến bằng 8, suy ra :
y' = 8 ⇔ 4$x^{3}$ + 4x - 8 = 0
⇔ 4(x - 1)($x^{2}$ + x + 2) = 0 ⇔ x = 1
Theo câu a), ta được phương trình tiếp tuyến phải tìm là : y = 2(4x - 3)
d) Cách 1: Phương trình tiếp tuyến tại điểm M($x_{0}$; f($x_{0}$)) của đồ thị (C) là
.png)
Vì tiếp tuyến phải tìm đi qua điểm A(0;-6) nên ta có :
.png)
Theo câu a) phương trình của hai tiếp tuyến phải tìm lần lượt là :
y = 2(4x - 3) và y = - 2(4x + 3)
Cách 2: Phương trình đường thẳng (l) đi qua điểm A(0; -6) với hệ số góc bằng k là : y = kx - 6
Để đường thẳng (l) là tiếp tuyến của đồ thị (C) (hay tiếp xúc với đồ thị (C)) thì ta phải tìm k sao cho :
.png)
Khử k từ hệ trên ta được : .png)
Suy ra .png)
Vậy hai tiếp tuyến phải tìm có phương trình là : y = 2(4x - 3) và y = -2(4x + 3)
54. Tìm một điểm trên đồ thị của hàm số .png)
sao cho tiếp tuyến tại đó cùng với các trục tọa độ tạo thành một tam giác có diện tích bằng 2.
Giải
.png)
Với mọi x $\neq$ 1, ta có : .png)
Phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm .png)
(với $x_{0}$ $\neq$ 1) là :
.png)
Tiếp tuyến này cắt trục hoành tại điểm A có hoành độ $x_{A}$ thỏa mãn :
.png)
và cắt trục tung tại điểm B có tung độ $y_{B}$ là :
.png)
Ta có: .png)
Suy ra .png)
Vậy điểm phải tìm $M_{0}$ có tọa độ là .png)
55. Đồ thị (P) của một hàm số bậc hai y = P(x) đã bị xóa đi, chỉ còn lại trục đối xứng $\Delta$, điển A thuộc (P) và tiếp tuyến tại A của (P). Hãy tìm P(x) và vẽ lại đồ thị (P)
.png)
Giải
Đa thức phải tìm có dạng : P(x) = a$x^{2}$ + bx + c (a $\neq$ 0).
Ta có : P'(x) = 2ax + b
Vì trục đối xứng ($\Delta$) có phương trình x = 1 nên : .png)
(1)
Vì đồ thị (P) đi qua điểm A(3; 0) nên ta có P(3) = 0, tức là :
9a + 3b + c = 0 (2)
Vì hệ số góc của tiếp tuyến tại điểm A(3; 0) bằng .png)
nên ta có P'(3) = 1, tức là : 6a + b = 1 (3)
Giải hệ ba phương trình (1), (2) và (3) với ba ẩn số a, b và c, ta được :
.png)
.png)
55. Cho parabol (P) : y = $x^{2}$. Gọi $M_{1}$ và $M_{2}$ là hai điểm thuộc (P), lần lượt có hoành độ là $x_{1}$ = - 2 và $x_{2}$ = 1. Hãy tìm trên (P) một điểm C sao cho tiếp tuyến tại C song song với cát tuyến $M_{1}M_{2}$. Viết phương trình của tiếp tuyến đó.
Giải
.png)
Các điểm $M_{1}$ và $M_{2}$ có tọa độ là $M_{1}$(-2; 4); $M_{2}$(1; 1).
Hệ số góc của cát tuyến $M_{1}M_{2}$ là .png)
Vì tiếp tuyến tại điểm C($x_{0}$; $x_{0}^{2}$) song song với cát tuyến $M_{1}M_{2}$ nên ta có :
.png)
Suy ra tọa độ của điểm C là .png)
Vậy phương trình tiếp tuyến phải tìm là :
.png)
57. Một chất điểm chuyển động có phương trình
s = $t^{3}$ - 3$t^{2}$ - 9t + 2, ở đó, t tính bằng giây (s) t > 0 và s tính bằng mét (m).
a) Tính vận tốc tại thời điểm t = 2;
b) Tính gia tốc tại thời điểm t = 3;
c) Tính gia tốc tại thời điểm vận tốc bằng 0;
d) Tính vận tốc tại thời điểm gia tốc bằng 0.
Giải
Ta có s' = 3$t^{2}$ - 6t - 9; s" = 6t - 6
a) Vận tốc tại thời điểm t = 2 là : v = s'(2) = - 9m/s
b) Gia tốc tại thời điểm t = 3 là : a = s”(3) = 12 m/$s^{2}$
c) v = s' = 0 ⇔ 3$t^{2}$ - 6t - 9 = 0 ⇔ t = 3
a(3) = s"(3) = 12m/$s^{2}$
d) a = s" = 0 ⇔ 6t - 6 = 0 ⇔ t = 1
v(1) = s'(1) = - 12m/s