§3. NHỊ THỨC NIU-TƠN
A. TÓM TẮT GIÁO KHOA
1. Công thức nhị thức Niu-tơn:
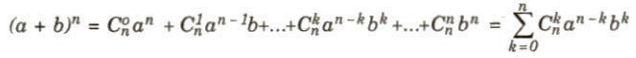
2. Tam giác Pa-xcan:
Muốn khai triển $(a+b)^{n}$ thành đa thức, ta cần biết n + 1 số $C_{n}^{0}$, $C_{n}^{1}$, $C_{n}^{2}$, ..., $C_{n}^{n-1}$, $C_{n}^{n}$ có mặt trong công thức nhị thức Niu-tơn. Các số này có thể tính được nhờ công thức ở §2. Ngoài ra còn có thể tìm được chúng bằng cách sử dụng bảng số sau đây :
.png)
Tam giác Pa-xcan được lập theo quy luật sau :
- Đỉnh được ghi số 1. Tiếp theo là hàng thứ nhất ghi hai số 1.
- Nếu biết hàng thứ n (n $\geq$ 1) thì hàng thứ n + 1 tiếp theo được thiết lập bằng cách cộng hai số liên tiếp của hàng thứ n rồi viết kết quả xuống hàng dưới ở vị trí giữa hai số này. Sau đó viết số 1 ở đầu và cuối hàng.
