§5. CÁC QUI TẮC TÍNH XÁC SUẤT
B. PHƯƠNG PHÁP GIẢI BÀI TẬP
34. Gieo ba đồng xu cân đối một cách độc lập. Tính xác suất để :
a) Cả ba đồng xu đều sấp ;
b) Có ít nhất một đồng xu sấp;
c) Có đúng một đồng xu sấp.
Giải
a) Gọi $A_{i}$ là biến cố "Đồng xu thứ i sấp” (i = 1, 2, 3), ta có P($A_{1}$) = $\large \frac{1}{2}$. Các biến cố $A_{1}$, $A_{2}$, $A_{3}$ độc lập. Theo quy tắc nhân xác suất, ta có : 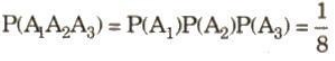
b) Gọi H là biến cố "Có ít nhất một đồng xu sấp". Biến cố đối của biến cố H là $\bar{H}$: "Cả ba đồng xu đều ngửa". Tương tự như câu a) ta có .png) . Vậy:
. Vậy:
.png)
c) Gọi K là biến cố "Có đúng một đồng xu sấp”. Ta có :
.png)
Theo quy tắc cộng xác suất, ta có :
.png)
Theo quy tắc nhân xác suất, ta tìm được :
.png)
.png)
35. Xác suất bắn trúng hồng tâm của một người bắn cung là 0,2. Tính xác suất để trong ba lần bắn độc lập :
a) Người đó bắn trúng hồng tâm đúng một lần;
b) Người đó bắn trúng hồng tâm ít nhất một lần.
Giải
a) Gọi $A_{i}$ là biến cố "Người bắn cung bắn trúng hồng tâm ở lần thứ i" (i = 1, 2, 3), ta có P($A_{i}$) = 0,2. Gọi K là biến cố "Trong ba lần bắn có duy nhất một lần người đó bắn trúng hồng tâm", ta có :
.png)
Theo qui tắc cộng xác suất, ta có :
.png)
Theo qui tắc nhân xác suất ta có :
.png)
Tương tự .png)
Vậy P(K) = 3.0,128 = 0,384.
b) Gọi H là biến cố “Trong ba lần bắn, người đó bắn trúng hồng tâm ít nhất một lần". Biến cố đối của biến cố H là $\bar{H}$ "Cả ba lần bắn, người đó đều bắn không trúng hồng tâm". Ta có : $\bar{H}$ = $\bar{A_{1}}$ $\bar{A_{2}}$ $\bar{A_{3}}$.
Theo quy tắc nhân xác suất, ta có :
P($\bar{A_{1}}$ $\bar{A_{2}}$ $\bar{A_{3}}$) = 0,8 . 0,8. 0,8 = 0,512
Vậy p(H) = 1 - P($\bar{H}$) = 1 - 0,512 = 0,488.
36. Gieo hai đồng xu A và B một cách độc lập. Đồng xu A chế tạo cân đối. Đồng xu B chế tạo không cân đối nên xác suất xuất hiện mặt sấp gấp ba lần xác suất xuất hiện mặt ngửa. Tính xác suất để:
a) Khi gieo hai đồng xu một lần thì cả hai đồng xu đều ngửa;
b) Khi gieo hai đồng xu hai lần thì cả hai đồng xu đều ngửa.
Giải
Gọi $A_{1}$ là biến cố "Đồng xu A sấp", $A_{2}$ là biến cố "Đồng xu A ngửa", $B_{1}$ là biến cố "Đồng xu B sấp", $B_{2}$ là biến cố "Đồng xu B ngửa".
Theo bài ra ta có : P($A_{1}$) = P($A_{2}$) = 0,5; P($B_{1}$) = 0,75; P($B_{2}$) = 0,25
a) $A_{2}B_{2}$ là biến cố "Cả hai đồng xu A và B đều ngửa". Theo qui tắc nhân xác suất, ta có :
.png)
b) Gọi $H_{1}$ là biến cố "Khi gieo hai đồng xu lần đầu thì cả hai đồng xu đều ngửa", $H_{2}$ là biến cố "Khi gieo hai đồng xu lần thứ hai thì cả hai đồng xu đều ngửa". Khi đó $H_{1}H_{2}$ là biến cố "Khi gieo hai đồng xu hai lần thì hai lần cả hai đồng xu đều ngửa".
Từ câu a) ta có .png)
Áp dụng quy tắc nhân xác suất, ta có :
.png)
37. Trong một bài thi trắc nghiệm khách quan có 10 câu. Mỗi câu có 5 phương án trả lời, trong đó chỉ có một phương án đúng. Một học sinh không học bài nên làm bài bằng cách với mỗi câu đều chọn ngẫu nhiên một phương án trả lời. Tính xác suất để học sinh đó trả lời không đúng cả 10 câu (tính chính xác đến hàng phần vạn).
Giải
Gọi $A_{i}$ là biến cố "Học sinh đó trả lời không đúng câu thứ i" với i = 1,...,10. Khi đó $A_{1}A_{2}...A_{10}$ là biến cố "Học sinh đó trả lời không đúng cả 10 câu". Từ giả thiết ta có P($A_{i}$) = 0,8.
Áp dụng qui tắc nhân xác suất, ta có :
.png)
38. Có hai hòm đựng thẻ, mỗi hòm đựng 12 thẻ đánh số từ 1 đến 12. Từ mỗi hòm rút ngẫu nhiên một thẻ. Tính xác suất để trong hai thẻ rút ra có ít nhất một thẻ đánh số 12.
Giải
Gọi A là biến cố "Thẻ rút từ hòm thứ nhất không đánh số 12", B là biến cố "Thẻ rút từ hòm thứ hai không đánh số 12". Ta có .png)
Gọi H là biến cố "Trong hai thẻ rút từ hai hòm có ít nhất một thẻ đánh số 12". Khi đó biến cố đối của biến cố H là $\bar{H}$: "Cả hai thẻ rút từ hai hòm đều không đánh số 12". Vậy $\bar{H}$ = AB. Theo qui tắc nhân xác suất, ta có :
.png)
39. Cho P(A) = 0,3; P(B) = 0,4 và P(AB) = 0,2. Hỏi hai biến cố A và B có :
a) Xung khắc hay không ?
b) Độc lập với nhau hay không ?
Giải
a) Vì P(AB) = 0,2 $\neq$ 0 nên hai biến cố A và B không xung khắc.
b) Ta có P(A)P(B) = 0,12. Vì P(AB) = 0,2 $\neq$ 0,12 = P(A)P(B) nên hai biến cố A và B không độc lập với nhau.
40. Trong một trò chơi điện tử, xác suất để An thắng một trận là 0,4. Hỏi An phải chơi tối thiểu bao nhiêu trận để trong loạt chơi đó xác suất thắng ít nhất một trận lớn hơn 0,95 ?
Giải
Gọi n là số trận mà An chơi. A là biến cố "An thắng ít nhất một trận trong loạt chơi n trận". Biến cố A là $\bar{A}$: "An thua cả n trận". Ta có P($\bar{A}$) = $(0,6)^{n}$
Vậy P(A) = 1 - $(0,6)^{n}$. Ta cần tìm số nguyên dương n nhỏ nhất thỏa mãn. PA $\geq$ 0,95 tức là 0,5 $\geq$ $(0,6)^{n}$.
Ta có $(0,6)^{5}$ $\approx$ 0,078; $(0,6)^{6}$ $\approx$ 0,047. Vậy n nhỏ nhất là 6. Thành thử An phải chơi tối thiểu 6 trận.
41. Gieo hai con súc sắc cân đối một cách độc lập. Tính xác suất để tổng số chấm trên mặt xuất hiện của hai con súc sắc bằng 8.
Giải
Gọi B là biến cố "Tổng số chấm trên mặt xuất hiện của hai con súc sắc là 8".
Tập hợp mô tả biến cố B gồm 5 phần tử :
$\Omega _{B}$ = {(2; 6), (6; 2), (3; 5), (5; 3), (4; 4)}
và không gian mẫu $\Omega$ có 36 phần tử
Khi đó .png)
42. Gieo ba con súc sắc cân đối một cách độc lập. Tính xác suất để tổng số chấm trên mặt xuất hiện của ba con súc sắc bằng 9.
Giải
Giả sử T là phép thử "Gieo ba con súc sắc".
Kết quả của T là bộ ba số (x, y, z), trong đó x, y, z tương ứng là kết quả của việc gieo con súc sắc thứ nhất, thứ hai, thứ ba. Không gian mẫu T có 6.6.6 = 216 phần tử. Gọi A là biến cố "Tổng số chấm trên mặt xuất hiện của ba con súc sắc là 9”. Ta có tập hợp các kết quả thuận lợi cho A là :
.png)
Nhận xét: 9 = 1 + 2 + 6 = 1 + 3 + 5 = 2 + 3 + 4 = 1+ 4 + 4 = 2 + 2 + 5 = 3 + 3 + 3
Tập {1, 2, 6} cho ta 6 phần tử của $\Omega_{A}$ là (1, 2, 6), (1, 6, 2), (6, 1, 2), (6, 2, 1), (2, 1, 6), (2, 6, 1).
Tương tự các tập {1, 3, 5}, {2, 3, 4}, mỗi tập cho ta 6 phần tử của $\Omega_{A}$; các tập {1, 4, 4}, {2, 2, 5}, mỗi tập cho ta 3 phần tử của $\Omega_{A}$, tập {3, 3, 3} cho ta duy nhất một phần tử của $\Omega_{A}$.
Vậy $\mid$$\Omega_{A}$$\mid$ = 6 + 6 + 6 + 3 + 3 + 1 = 25
Suy ra .png)
BÀI TẬP LÀM THÊM
Cho hai hộp bị. Hộp thứ nhất có 7 bi xanh và 3 bi đỏ. Hộp thứ hai có 6 bi xanh và 4 bi đỏ. Từ mỗi hộp lấy ra 1 viên bi. Tính xác suất để:
1) Được 1 bi xanh và 1 bi đỏ.
2) Được 2 bi đỏ.
3) Được ít nhất 1 bi đỏ.
ĐS: $A_{1}$: Biến cố lấy ở hộp thứ nhất là đỏ.
$A_{2}$: biến cố lấy ở hộp thứ hai là đỏ.
1) A = $A_{1}\bar{A_{2}}$ + $\bar{A_{1}}A_{2}$ là biến cố lấy 1 xanh và 1 đỏ
.png)
.png)
