Chương 5. ĐẠO HÀM

§1. KHÁI NIỆM ĐẠO HÀM

A. TÓM TẮT GIÁO KHOA

1. Đạo hàm của hàm số tại một điểm :

Khái niệm đạo hàm của hàm số tại một điểm:

Cho hàm số y = f(x) xác định trên khoảng (a; b) và điểm $x_{0}$ thuộc khoảng đó.

Định nghĩa : Giới hạn hữu hạn (nếu có) của tỉ số 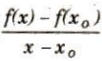khi x dần đến $x_{0}$ được gọi là đạo hàm của hàm số đã cho tại điểm $x_{0}$, kí hiệu là f'($x_{0}$) hoặc y'($x_{0}$), nghĩa là :

Trong định nghĩa trên, nếu đặt $\Delta x$ = x - $x_{0}$ và $\Delta y$ = f($x_{0}$ + $\Delta x$) - f($x_{0}$) thì ta có:

Chú ý:

1) $\Delta x$ được gọi là số gia của biến số tại $x_{0}$; số $\Delta y$ được gọi là số gia của hàm số ứng với số gia $\Delta x$ tại $x_{0}$.

2. Qui tắc tính đạo hàm theo định nghĩa :

Qui tắc:

Muốn tính đạo hàm của hàm số f tại điểm $x_{0}$ theo định nghĩa, ta thực hiện hai bước sau:

• Bước 1: Tính $\Delta y$ theo công thức $\Delta y$ = f($x_{0}$ + $\Delta x$) - f($x_{0}$), trong đó $\Delta x$ là số gia của biến số tại $x_{0}$

• Bước 2: Tìm giới hạn lim

3. Ý nghĩa hình học của đạo hàm :

Đạo hàm của hàm số y = f(x) tại điểm $x_{0}$ là hệ số góc của tiếp tuyến của đồ thị hàm số đó tại điểm $M_{0}(x_{0};f(x_{0}))$

Chú ý:

Nếu hàm số y = f(x) có đạo hàm tại điểm $x_{0}$ thì tiếp tuyến của đồ thị hàm số tại điểm $M_{0}(x_{0};f(x_{0}))$ có phương trình là :

y = f'($x_{0}$)(x - $x_{0}$) + f($x_{0}$)

4. Ý nghĩa cơ học của đạo hàm:

Vận tốc tức thời v($t_{0}$) tại thời điểm $t_{0}$ của một chuyển động có phương trình s = s(t) bằng đạo hàm của hàm số s = s(t) tại điểm $t_{0}$, tức là : v($t_{0}$) = s'($t_{0}$)

5. Đạo hàm của hàm số trên một khoảng :

a) Khái niệm :

- Cho hàm số f xác định trên tập J, trong đó J là một khoảng hoặc là hợp của những khoảng nào đó.

Định nghĩa:

1) Hàm số f gọi là có đạo hàm trên J nếu nó có đạo hàm f'(x) tại mọi điểm x thuộc J.

2) Nếu hàm số f có đạo hàm trên J thì hàm số f xác định bởi

f': J → R

x $\mapsto$ f'(x)

gọi là đạo hàm của hàm số f.

Đạo hàm của hàm số y = f(x) cũng được kí hiệu bởi y'.

b) Đạo hàm của một số hàm số thường gặp:

Định lí:

a) Hàm số hằng y = c' có đạo hàm trên R và y' = 0

b) Hàm số y = x có đạo hàm trên R và y' = 1;

c) Hàm số y = x” (n $\in$ N, n ≥ 2) có đạo hàm trên R và y' = n$x^{n-1}$

d) Hàm số y = $\sqrt{x}$ có đạo hàm trên khoảng (0; +$\infty$) và