§3. DÃY SỐ CÓ GIỚI HẠN VÔ CỰC

A. TÓM TẮT GIÁO KHOA

1. Dãy số có giới hạn $+\infty$:

Định nghĩa:

Dãy số ($u_{n}$) có giới hạn +$\infty$ nếu với mỗi số dương tùy ý cho trước, mọi số hạng của dãy số, kể từ số hạng nào đó trở đi, đều lớn hơn số dương đó.

Khi đó ta viết :

lim($u_{n}$) = +$\infty$ hoặc lim$u_{n}$ = +$\infty$ hoặc $u_{n}$ → +$\infty$

Chú ý : limn = +$\infty$, lim$\sqrt{n}$ = +$\infty$, lim$\sqrt[k]{n}$ = +$\infty$ (k $\in$ N*)

2. Dãy số có giới hạn -$\infty$:

Định nghĩa :

Dãy số ($u_{n}$) có giới hạn -$\infty$ nếu với mỗi số âm tùy ý cho trước, mọi số hạng của dãy số, kể từ số hạng nào đó trở đi, đều nhỏ hơn số âm đó.

Khi đó ta viết :

lim($u_{n}$) = -$\infty$ hoặc lim$u_{n}$ = -$\infty$ hoặc $u_{n}$ → -$\infty$

Định lí:

Nếu lim $\mid$$u_{n}$$\mid$ = +$\infty$ thì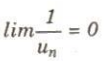

3. Một vài qui tắc tìm giới hạn vô cực :

a) Qui tắc 1:

Nếu thì lim($u_{n}v_{n}$) được cho trong bảng sau:

b) Qui tắc 2:

Nếu thì lim($u_{n}v_{n}$) được cho trong bảng sau :

c) Qui tắc 3:

Nếu lim$u_{n}$ = L $\neq$ 0, lim$v_{n}$ = 0 và $v_{n}$ > 0 hoặc $v_{n}$ < 0 kể từ một số hạng nào đó trở đi thì được cho trong bảng sau :