Các quy tắc tính đạo hàm (tóm tắt giáo khoa)

§2. CÁC QUI TẮC TÍNH ĐẠO HÀM

A. TÓM TẮT GIÁO KHOA

1. Đạo hàm của tổng hay hiệu hai hàm số:

Định lí 1:

Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm trên J thì hàm số y = u(x) + v(x) và y = u(x) - v(x) cũng có đạo hàm trên J, và :

a) [u(x) + v(x)]' = u'(x) + v'(x);

b) [u(x) - v(x)]' = u'(x) - v'(x)

Các công thức trên có thể viết gọn là :

(u + v)' = u' + v' và (u - v)' = u' - v'

2. Đạo hàm của tích hai hàm số :

Định lí 2:

Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm trên J thì hàm số y = u(x)v(x) cũng có đạo hàm trên J, và :

[u(x)v(x)]' = u'(x).v(x) + u(x)v'(x);

Đặc biệt, nếu k là hằng số thì [ku(x)]' = ku'(x)

Các công thức trên có thể viết gọn là :

(uv)' = u'v + uv' và (ku)' = ku'

3. Đạo hàm của thương hai hàm số :

Định lí 3:

Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm trên J và v(x) $\neq$ 0 với mọi x $\in$ J thì hàm số 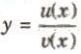cũng có đạo hàm trên J và

Công thức trên có thể viết gọn là :

Hệ quả :

a) Trên (-$\infty$; 0) $\cup$ (0; +$\infty$) ta có

b) Nếu hàm số v = v(x) có đạo hàm trên J và v(x) $\neq$ 0 với mọi x thuộc J thì trên J ta có

Công thức thứ hai trong hệ quả trên có thể viết gọn là :

4. Đạo hàm của hàm số hợp:

a) Khái niệm hàm số hợp:

Cho hai hàm số y = f(u) và u = u(x). Thay biến u trong biểu thức f(u) bởi biểu thức u(x), ta được biểu thức f[u(x)] với biến x. Khi đó, hàm số y = g(x) với g(x) = f[u(x)] được gọi là hàm số hợp của hai hàm số f và u; hàm số u gọi là hàm số trung gian. (Tất nhiên, ta chỉ xét các giá trị của biến x sao cho f[u(x)] là xác định).

b) Cách tính đạo hàm của hàm số hợp:

Định lí 4:

a) Nếu hàm số u = u(x) có đạo hàm tại điểm $x_{0}$ và hàm số y = f(u) có đạo hàm tại điểm $u_{0}$ = u($x_{0}$) thì hàm số hợp g(x) = f[u(x)] có đạo hàm tại điểm $x_{0}$ và g'($x_{0}$) = f'($u_{0}$).u'($x_{0}$)

b) Nếu giả thiết trong phần a) được thỏa mãn đối với mọi điểm x thuộc J thì hàm số hợp y = g(x) có đạo hàm trên J và g'(x) = f'[u(x)].u'(x)

Công thức thứ hai trong định lý trên còn được viết gọn là :

$g'_{x}=f'_{u}.u'_{x}$

Hệ quả 1:

Nếu hàm số u = u(x) có đạo hàm trên J thì hàm số y = u''(x) (với n $\in$ N và n ≥ 2) có đạo hàm trên J và