§2. DÃY SỐ

B. PHƯƠNG PHÁP GIẢI BÀI TẬP

a) Xét tính đơn điệu của dãy số :

b) Chứng minh dãy số ($u_{n}$) không tăng không giảm :

• Chỉ ra rằng $u_{1}$ < $u_{2}$ > $u_{3}$ hoặc $u_{1}$ > $u_{2}$ < $u_{3}$

• Thường là dãy số có số hạng $(-1)^{n}$.

c) Dãy số bị chặn:

($u_{n}$) bị chặn trên ⇔ $\exists$M sao cho $u_{n}$ $\leq$ M, $\forall$n $\in$ $Z^{+}$

($u_{n}$) bị chặn dưới ⇔ $\exists$m sao cho $u_{n}$ $\geq$ m, $\forall$n $\in$ $Z^{+}$

($u_{n}$) bị chặn ⇔ $\exists$M > 0 sao cho $\mid u_{n}\mid$ $\leq$ M, $\forall$n $\in$ $Z^{+}$

9. Tìm 5 số hạng đầu của mỗi dãy số sau :

Giải

10. Tìm số hạng thứ 3 và số hạng thứ 5 của mỗi dãy số sau :

a) Dãy số ($u_{n}$) xác định bởi :

b) Dãy số ($u_{n}$) xác định bởi :

Giải

11. Cho hình vuông $A_{1}B_{1}C_{1}D_{1}$ có cạnh bằng 6cm. Người ta dựng các hình vuông $A_{2}B_{2}C_{2}D_{2}$, $A_{3}B_{3}C_{3}D_{3}$,..., $A_{n}B_{n}C_{n}D_{n}$,... theo cách sau: Với mỗi n = 2, 3, 4,... lấy các điểm $A_{n}$, $B_{n}$, $C_{n}$ và $D_{n}$ tương ứng trên các cạnh $A_{n-1}B_{n-1}$, $B_{n-1}C_{n-1}$, $C_{n-1}D_{n-1}$ và $D_{n-1}A_{n-1}$ sao cho $A_{n-1}A_{n}$ = 1cm và $A_{n}B_{n}C_{n}D_{n}$ là một hình vuông. Xét dãy số ($u_{n}$) với $u_{n}$ là độ dài cạnh của hình vuông $A_{n}B_{n}C_{n}D_{n}$

Hãy cho dãy số ($u_{n}$) nói trên bởi một hệ thức truy hồi.

Giải

Với mỗi n $\in$ N*, xét các hình vuông $A_{n}B_{n}C_{n}D_{n}$ và $A_{n+1}B_{n+1}C_{n+1}D_{n+1}$, ta có

12. Cho dãy số ($u_{n}$) xác định bởi :

$u_{1}$ = 1 và $u_{n}$ = 2$u_{n-1}$ + 3 với mọi n $\geq$ 2

Bằng phương pháp quy nạp, chứng minh rằng với mọi n $\geq$ 1 ta có:

$u_{n}$ = $2^{n+1}$ - 3 (1)

Giải

Với n = 1 ta có $u_{1}$ = 1 = $2^{2}$ - 3. Vậy (1) đúng với n = 1

Giả sử (1) đúng với n - k tức là ta có : $u_{k}$ = $2^{k+1}$ - 3

Ta chứng minh (1) đúng với n = k + 1, tức là phải chứng minh :

Thật vậy theo giả thiết qui nạp ta có :

Vậy (1) đúng với n = k + 1 do đó (1) đúng với mọi n $\in$ N*.

13. Hãy xét tính tăng, giảm của các dãy số sau :

a) Dãy số ($u_{n}$) với

b) Dãy số ($x_{n}$) với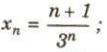

c) Dãy số ($a_{n}$) với

Hướng dẫn :

a) Xét hiệu $u_{n+1}-u_{n}$

b) Xét tỉ số

c) Viết lại công thức xác định $a_{n}$ dưới dạng

Tiếp theo, xét tỉ số

Giải

a) Ta có :

14. Chứng minh rằng dãy số ($u_{n}$) với là một dãy số giảm và bị chặn.

Giải

Vậy ($u_{n}$) là dãy số giảm và bị chặn.

15. Cho dãy số ($u_{n}$) xác định bởi :

$u_{1}$ = 3 và $u_{n+1}$ = $u_{n}$ + 5 với mọi n $\geq$ 1.

a) Hãy tính $u_{2}$, $u_{4}$ và $u_{6}$;

b) Chứng minh rằng $u_{n}$ = 5n - 2 với mọi n $\geq$ 1.

Giải

a) Ta có $u_{2}$ = $u_{1}$ + 5 = 8; $u_{3}$ = $u_{2}$ + 5 = 13 ;

$u_{4}$ = $u_{3}$ + 5 = 18; $u_{5}$ = $u_{4}$ + 5 = 23; $u_{6}$ = $u_{5}$ + 5 = 28

b) Ta sẽ chứng minh : $u_{n}$ = 5n - 2 (1) với mọi n $\in$ N*, bằng phương pháp qui nạp.

Với n = 1, ta có $u_{1}$ = 3 = 5.1 - 2

Như thế (1) đúng khi n = 1

Giả sử (1) đúng khi n = k, k $\in$ N*, ta sẽ chứng minh nó cũng đúng khi n = k + 1

Thật vậy, từ công thức xác định dãy số ($u_{n}$) và giả thiết qui nạp ta có :

$u_{k+1}$ = $u_{k}$ + 5 = 5k - 2 + 5 = 5(k + 1) - 2

Từ các chứng minh trên suy ra (1) đúng với mọi n $\in$ N*.

* Cách khác :

16. Cho dãy số ($u_{n}$) xác định bởi :

$u_{1}$ = 1 và $u_{n+1}$ = $u_{n}$ + (n + 1).$2^{n}$ với mọi n $\geq$ 1.

a) Chứng minh rằng ($u_{n}$) là một dãy số tăng ;

b) Chứng minh rằng $u_{n}$ = 1 + (n - 1).$2^{n}$ với mọi n $\geq$ 1.

Giải

a) Từ hệ thức xác định dãy số ($u_{n}$), ta có :

Do đó ($u_{n}$) là một dãy số tăng.

b) Ta sẽ chứng minh $u_{n}$ = 1 + (n - 1).$2^{n}$ (1) với mọi n $\geq$ 1, bằng phương pháp qui nạp.

Với n = 1, ta có $u_{1}$ = 1 = 1 + (1 - 1).$2^{1}$. Như vậy (1) đúng khi n = 1

Giả sử (1) đúng khi n = k, k $\in$ N*, ta sẽ chứng minh nó cũng đúng khi n = k + 1.

Thật vậy, từ hệ thức xác định dãy số ($u_{n}$) và giả thiết qui nạp, ta có :

Từ các chứng minh trên suy ra (1) đúng với mọi n $\geq$ 1.

17. Cho dãy số ($u_{n}$) xác định bởi : $u_{1}$ = 1 và với mọi n $\geq$ 1.

Chứng minh rằng ($u_{n}$) là một dãy số không đổi (dãy số có tất cả các số hạng đều bằng nhau).

Giải

Ta chứng minh $u_{n}$ = 1 (1) $\forall n\in$ N* bằng qui nạp

Rõ ràng (1) đúng với n = 1

Giả sử (1) đúng với n = k, tức là ta có $u_{k}$ = 1

Ta chứng minh (1) đúng với n = k + 1, thật vậy ta có :

Vậy (1) đúng với n = k + 1, do đó (1) đúng với mọi n $\in$ N*

18. Cho dãy số ($s_{n}$) với

a) Chứng minh rằng $s_{n}$ = $s_{n+3}$ với mọi n $\geq$ 1;

b) Hãy tính tổng 15 số hạng đầu tiên của dãy số đã cho.

Giải

a) Với n là số nguyên dương tùy ý, ta có :

b) Từ kết quả phần a) ta có :

Từ đó suy ra:

C. BÀI TẬP LÀM THÊM

1. Viết 4 số hạng đầu của dãy ($a_{n}$):

2. Xét tính đơn điệu của các dãy ($a_{n}$)

Đáp số :

a) Tăng;

b) Không tăng, không giảm;

c) Tăng ;

d) Giảm ;

e) Tăng.

3. Xét tính bị chặn trên, bị chặn dưới của các dãy số :