§3. ĐẠO HÀM CỦA CÁC HÀM SỐ LƯỢNG GIÁC

A. TÓM TẮT GIÁO KHOA

1. Giới hạn: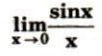

Định lí 1:

•

• Nếu hàm số u = u(x) thỏa mãn các điều kiện: u(x) $\neq$ 0 với mọi x $\neq$ $x_{0}$ và thì

2. Đạo hàm của hàm số y = sinx:

Định lí 2:

a) Hàm số y = sinx có đạo hàm trên R, và (sinx)' = cosx

b) Nếu hàm số u = u(x) có đạo hàm trên J thì trên J ta có :

[sin(u(x))]' = cos(u(x)). u'(x).

3. Đạo hàm của hàm số y = cosx :

Định lí 3:

a) Hàm số y = cosx có đạo hàm trên R và (cosx)' = - sinx

b) Nếu hàm số u = u(x) có đạo hàm trên J thì trên J ta có

cos(u(x))' = (-sin(u(x)). u'x

hay (cosu)' = - u'sinu

4. Đạo hàm của hàm số y = tanx:

Định lí 4:

a) Hàm số y = tanx có đạo hàm trên mỗi khoảng

(với k $\in$ Z), và

b) Giả sử hàm số u = u(x) có đạo hàm trên J và với mọi x $\in$ J. Khi đó, trên J ta có :

hay:

5. Đạo hàm của hàm số y = cotx :

Định lí 5:

a) Hàm số y = cotx có đạo hàm trên mỗi khoảng ($k\pi$; (k + 1)$\pi$) với (k $\in$ Z) và

b) Giả sử hàm số u = u(x) có đạo hàm trên J và u(x) $\neq$ $k\pi$ (k $\in$ Z) với mọi x $\in$ J. Khi đó trên J ta có:

hay: