Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
§1. CÁC HÀM SỐ LƯỢNG GIÁC
A. TÓM TẮT GIÁO KHOA
1. Các hàm số y = sinx và y = cosx:
a) Tập xác định
Tập xác định của hàm số y = sinx và y = cosx là D = R.
Hàm số y = sinx là hàm số lẻ.
Hàm số y = cosx là hàm số chẵn.
b) Tính chất tuần hoàn của các hàm số y = sinx và y = cosx
Hàm số y = sin x và y = cosx là hàm số tuần hoàn với chu kỳ 2$\pi$.
c) Sự biến thiên và đồ thị của hàm số y = sinx
* Bảng biến thiên của hàm số y = sinx trên đoạn [-$\pi$; $\pi$] như sau :
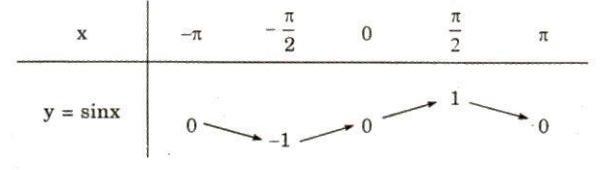
* Đồ thị hàm số y = sinx
.png)
d) Sự biến thiên và đồ thị của hàm số y = cosx.
* Bảng biến thiên của hàm số y = cosx trên đoạn [-$\pi$; $\pi$]
.png)
* Đồ thị hàm số y = cosx
Ta có : cosx = sin(x + $\large \frac{\pi }{2}$) với mọi x, nên bằng cách tịnh tiến đồ thị hàm số y = sinx sang trái một đoạn có độ dài $\large \frac{\pi }{2}$, ta được đồ thị hàm số y = cosx (nó cũng được gọi là một đường hình sin).
.png)
* Chú ý:
Hàm số y = sinx và y = cosx có tập xác định là R, tập giá trị là [-1; 1], là hàm số tuần hoàn có chu kì 2$\pi$ và có đồ thị là một đường sin.
2. Các hàm số y = tanx và y = cotx :
a) Tập xác định
• Hàm số y = tanx xác định với mọi x $\neq$ $\large \frac{\pi }{2}$ + k$\pi$ (k $\in$ Z)
Hàm số y = tanx là một hàm số lẻ.
• Hàm số y = cotx xác định với mọi x $\neq$ k$\pi$ (k $\in$ Z)
Hàm số y = cotx là một hàm số lẻ.
b) Tính chất tuần hoàn
Hàm số y = tanx và y = cotx là những hàm số tuần hoàn với chu kì $\pi$.
c) Đồ thị của hàm số y = tanx
.png)
d) Đồ thị của hàm số y = cotx
.png)
* Chú ý:
• Hàm số y = tanx có tập xác định .png)
Hàm số y = cotx có tập xác định .png)
• Hai hàm số y = tanx và y = cotx có tập giá trị là R, là hàm số lẻ và là các hàm tuần hoàn có chu kì $\pi$.
3. Về khái niệm hàm số tuần hoàn:
Hàm số y = f(x) xác định trên tập hợp $\wp$ được gọi là hàm số tuần hoàn nếu có số T $\neq$ 0 sao cho với mọi x $\in$ $\wp$ ta có:
x + T $\in$ $\wp$, x - T $\in$ $\wp$, và f(x + T) = f(x)
Nếu có số T dương nhỏ nhất thỏa mãn các điều kiện trên thị hàm số đó được gọi là một hàm số tuần hoàn mới chu kỳ T.
