§6. BIẾN NGẪU NHIÊN RỜI RẠC

A. TÓM TẮT GIÁO KHOA

1. Khái niệm biến ngẫu nhiên rời rạc:

Đại lượng X được gọi là một biến ngẫu nhiên rời rạc nếu nó nhận giá trị bằng số thuộc một tập hữu hạn nào đó và giá trị ấy là ngẫu nhiên, không dự đoán trước được.

2. Phân bố xác suất của biến ngẫu nhiên rời rạc:

Giả sử X = {$x_{1}$, $x_{2}$, ..., $x_{n}$}

Gọi $P_{i}$ = P(X = $x_{i}$) với i = 1, 2, ... , n

Ta lập bảng sau :

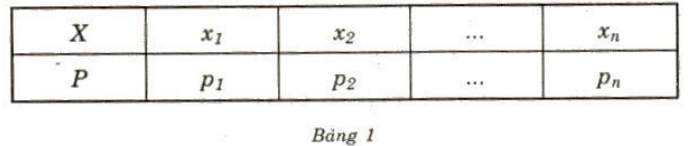
Bảng 1 được gọi là bảng phân bố xác suất của biến ngẫu nhiên rời rạc X.

Chú ý: $p_{1}$ + $p_{2}$ +...+ $p_{n}$ = 1

3. Kì vọng :

Định nghĩa:

Giả sử X = {$x_{1}$, $x_{2}$, ..., $x_{n}$}

được gọi là kì vọng của X;

đó $p_{i}$ = P(X = $x_{i}$), (i = 1, 2,..., n)

Ý nghĩa: E(X) là một số cho ta một ý niệm về độ lớn trung bình của X. Vì thế kì vọng E(X) còn được gọi là giá trị trung bình của X.

Nhận xét: Kì vọng của X không nhất thiết thuộc tập các giá trị của X.

4. Phương sai và độ lệch chuẩn:

a) Phương sai:

Định nghĩa:

Cho biến ngẫu nhiên rời rạc X = {$x_{1}$, $x_{2}$, ..., $x_{n}$}

được gọi là phương sai của X; ở đó $p_{i}$ = P(X = $x_{i}$)(i = 1, 2,...,n) và $\mu$ = E(X)

Ý nghĩa: Phương sai là một số không âm. Nó cho ta một ý niệm về mức độ phân tán các giá trị của X xung quanh giá trị trung bình. Phương sai càng lớn thì độ phân tán này càng lớn.

b) Độ lệch chuẩn:

Định nghĩa:

Căn bậc hai của phương sai, kí hiệu là $\sigma$(X), được gọi là độ lệch chuẩn của X.

Ta có : $\sigma$(X) = $\sqrt{V(X)}$.