Chương 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
§1. CÁC HÀM SỐ LƯỢNG GIÁC
B PHƯƠNG PHÁP GIẢI BÀI TẬP
1. Tìm tập xác định của mỗi hàm số sau:
.png)
Giải
a) Vì -1 $\leq$ sinx $\leq$ 1 nên 3 - sinx > 0 với mọi x nên tập xác định của hàm số là R. D = R
b) .png)
xác định khi và chỉ khi sinx $\neq$ 0
⇔ x $\neq$ $k\pi$, k $\in$ Z.
Vậy tập xác định D = R \ {$k\pi$ / k $\in$ Z}
c) Vì 1 - sinx $\geq$ 0 và 1 + cosx $\geq$ 0 nên hàm số xác định khi và chỉ khi cosx $\neq$ -1 ⇔ x $\neq$ $\pi$ + k2$\pi$, k $\in$ Z
Vậy tập xác định D = R \ {$\pi$ + k2$\pi$ / k $\in$ Z}
.png)
2. Xét tính chẵn - lẻ của mỗi hàm số sau :
a) y = - 2sinx;
b) y = 3sinx - 2;
c) y = sinx - cosx ;
d) y = sinx$cos^{2}$x + tanx
Giải
a) f(x) = -2sinx
Tập xác định D = R, ta có f(-x) = -2sin(-x) = 2sinx = - f(x), $\forall x\in R$
Vậy y = - 2sinx là hàm số lẻ.
b) f(x) = 3sinx - 2
Ta có : .png)
.png)
nên hàm số y = 3sinx - 2 không phải là hàm số chẵn cũng không phải là hàm số lẻ.
c) f(x) = sinx - cosx
Ta có .png)
.png)
nên y = sinx - cosx không phải là hàm số lẻ cũng không phải là hàm số chẵn.
d) f(x) = sinx$cos^{2}$x + tanx
Tập xác định .png)
$\forall x\in D$ ta có – x $\in$ D và f(-x) = sin(-x)$cos^{2}$(-x) + tan(-x)
= - sinx$cos^{2}$x - tanx = -f(x) nên hàm số đã cho là hàm số lẻ.
3. Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau :
.png)
Giải
.png)
.png)
4. Cho các hàm số f(x) = sinx, g(x) = cosx, h(x) = tanx và các khoảng
.png)
Hỏi hàm số nào trong ba hàm số đồng biến trên khoảng $J_{1}$? Trên khoảng $J_{2}$? Trên khoảng $J_{3}$? Trên khoảng $J_{4}$? (Trả lời bằng cách lập bảng).
Giải
Chú ý rằng .png)
Ta có bảng sau, trong đó dấu "+" có nghĩa "đồng biến", dấu "0" có nghĩa "không đồng biến":
.png)
5. Trong các khẳng định sau, khẳng định nào đúng ? Khẳng định nào sai ? Giải thích vì sao ?
a) Trên mỗi khoảng mà hàm số y = sinx đồng biến thì hàm số y = cosx nghịch biến.
b) Trên mỗi khoảng mà hàm số y = $sin^{2}$x đồng biến thì hàm số y = $cos^{2}$x nghịch biến.
Giải
a) Sai vì trên khoảng .png)
hàm số y = sinx đồng biến nhưng hàm số y = cosx không nghịch biến.
b) Đúng do $sin^{2}$x + $cos^{2}$x = 1
Giả sử y = $sin^{2}$x đồng biến trên khoảng I, khi đó với $x_{1}$, $x_{2}$ $\in$ I và $x_{1}$ < $x_{2}$ thì $sin^{2}x_{1}$ < $sin^{2}x_{2}$
⇒ 1 - $sin^{2}x_{1}$ > 1 - $sin^{2}x_{2}$ ⇒ $cos^{2}x_{1}$ > $cos^{2}x_{2}$
⇒ y = $cos^{2}$x nghịch biến trên I.
6. Cho hàm số y = f(x) = 2sin2x.
a) Chứng minh rằng với số nguyên k tùy ý, luôn có f(x + k$\pi$) = f(x) với mọi x
b) Lập bảng biến thiên của hàm số y = 2sin2x trên đoạn .png)
c) Vẽ đồ thị hàm số y = 2sin2x.
Giải
a) Ta có f(x + k$\pi$) = 2sin2(x + k$\pi$) = 2sin(2x + k2$\pi$) = 2sin2x = f(x), $\forall x\in R$.
b) Bảng biến thiên :
.png)
c) Đồ thị:
.png)
7. Xét tính chẵn lẻ của mỗi hàm số sau :
.png)
b) y = tan $\mid$x$\mid$;
c) y = tanx - sin2x
Giải
a) Ta có .png)
.png)
không phải là hàm số chẵn cũng không phải là hàm số lẻ.
b) f(x) = tan$\mid$x$\mid$.
Tập xác định .png)
x $\in$ D ⇒ -x $\in$ D và f(-x) = tan$\mid$-x$\mid$ = tan$\mid$x$\mid$ = f(x)
Do đó y = tan$\mid$x$\mid$ là hàm số chẵn.
c) f(x) = tanx - sin2x. Tập xác định .png)
x $\in$ D ⇒ - x $\in$ D và f(-x) = tan(-x) - sin(-2x)
= -tanx + sin2x = - (tanx - sin2x) = -f(x)
Do đó y = tanx - sin2x là hàm số lẻ.
8. Cho các hàm số sau :
.png)
Chứng minh rằng mỗi hàm số y = f(x) đó đều có tính chất :
f(x + k$\pi$) = f(x) với k $\in$ Z, x thuộc tập xác định của hàm số f.
Giải
Với k $\in$ Z ta có :
.png)
9. Cho hàm số y = f(x) = Asin($\omega$x + $\alpha$) (A, $\omega$ và $\alpha$ là các hằng số; A và $\omega$ khác 0). Chứng minh rằng với mỗi số nguyên k, ta có .png)
với mọi x.
Giải
Với k $\in$ Z ta có :
.png)
10. Chứng minh rằng mọi giao điểm của đường thẳng xác định bởi phương trình .png)
với đồ thị của hàm số y = sinx đều cách gốc tọa độ một khoảng nhỏ hơn $\sqrt{10}$.
Giải
Đường thẳng .png)
đi qua các điểm E(-3; - 1) và F(3; 1)
.png)
Chỉ có đoạn thẳng EF của đường thẳng đó nằm trong dải .png)
(dải này chứa đồ thị của hàm số y = sinx). Vậy các giao điểm của đường thẳng với đồ thị của hàm số y = sinx phải thuộc đoạn thẳng EF; mọi điểm của đoạn thẳng này cách O một khoảng không dài hơn $\sqrt{9+1}$ = $\sqrt{10}$ (và rõ ràng E, F không thuộc đồ thị của hàm số y = sinx).
11. Từ đồ thị của hàm số y = sinx, hãy suy ra đồ thị của các hàm số sau và vẽ đồ thị của các hàm số đó :
a) y = - sinx ;
b) y = $\mid$sinx$\mid$;
c) y = sin $\mid$x$\mid$.
Giải
a) Đồ thị của hàm số y = - sinx là hình đối xứng qua trục hoành của đồ thị hàm số y = sinx
.png)
b)
.png)
do đó đồ thị của hàm số y = $\mid$sinx$\mid$ có được từ đồ thị (C) của hàm số y = sinx bằng cách :
- Giữ nguyên phần đồ thị của (C) nằm trong nửa mặt phẳng y $\geq$ 0 (tức là nửa mặt phẳng bên trên trục hoành kể cả bờ Ox).
- Lấy hình đối xứng qua trục hoành của phần đồ thị (C) nằm trong nửa mặt phẳng y < 0 (tức là nửa mặt phẳng bên dưới trục hoành không kể bờ Ox);
- Xóa phần đồ thị của (C) nằm trong nửa mặt phẳng y < 0.
- Đồ thị y = $\mid$sinx$\mid$ là đường liền nét trong hình dưới đây :
.png)
c)
Ta có: .png)
do đồ thị của hàm số y = sin$\mid$x$\mid$ có được từ đồ thị (C) của hàm số y = sinx bằng cách:
- Giữ nguyên phần đồ thị của (C) nằm trong nửa mặt phẳng x $\geq$ 0 (tức nửa mặt phẳng bên phải trục tung kể cả bờ Oy).
- Xoá phần đồ thị của (C) nằm trong nửa mặt phẳng x < 0 (tức nửa mặt phẳng bên trái trục tung không kể bờ Oy).
- Lấy hình đối xứng qua trục tung của phần đồ thị (C) nằm trong nửa mặt phẳng x > 0.
- Đồ thị y = sin$\mid$x$\mid$ là đường nét liền trong hình dưới đây:
.png)
12. a) Từ đồ thị hàm số y = cosx, hãy suy ra đồ thị của hàm số sau và vẽ đồ thị của các hàm số đó:
.png)
b) Hỏi mỗi hàm số đó có phải là hàm số tuần hoàn không?
Giải
a) Đồ thị của hàm số y = cosx + 2 có được do tịnh tiến đồ thị của hàm số y = cosx lên trên một đoạn có độ dài bằng 2, tức là tịnh tiến theo vectơ 2$\vec{j}$ ($\vec{j}$ = (0,1) là vectơ đơn vị trên trục tung).
.png)
Đồ thị của hàm số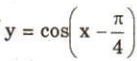 
có được do tịnh tiến đồ thị của hàm số y = cosx sang phải một đoạn có độ dài $\large \frac{\pi }{4}$, tức là tịnh tiến theo vectơ $\large \frac{\pi }{4}\vec{i}$ ($\vec{i}$ = (1, 0) là vectơ đơn vị trên trục hoành).
.png)
b) Các hàm số trên đều là hàm tuần hoàn vì :
.png)
13. Xét hàm số .png)
a) Chứng minh rằng với mỗi số nguyên k, f(x + k4$\pi$) = f(x) với mọi x.
b) Lập bảng biến thiên của hàm số y = cos$\large \frac{x}{2}$ trên đoạn [-2$\pi$; 2$\pi$]
c) Vẽ đồ thị của các hàm số y = cosx và y = cos$\large \frac{x}{2}$ trong cùng một hệ tọa độ vuông góc Oxy.
d) Trong mặt phẳng tọa độ Oxy, xét phép biến hình $\tau$ biến mỗi điểm (x; y) thành điểm (x'; y') sao cho x' = 2x và y' = y. Chứng minh rằng $\tau$ biến đồ thị của hàm số y = cosx thành đồ thị của hàm số y = cos$\large \frac{x}{2}$
Giải
.png)
b) Bảng biến thiên :
.png)
c)
.png)
d) Nếu đặt x' = 2x, y' = y thì y = cosx khi và chỉ khi y' = cos$\large \frac{x'}{2}$. Do đó phép biến đổi xác định bởi (x; y) $\mapsto$ (x'; y') sao cho x' = 2x, y' = y biến đồ thị hàm số y = cosx thành đồ thị hàm số y = cos$\large \frac{x}{2}$
.png)
C. BÀI TẬP LÀM THÊM
1. Tìm tập xác định của các hàm số sau :
.png)
2. Xét tính chẵn lẻ của các hàm số:
.png)
ĐS:
a) Hàm số chẵn;
b) Hàm số chẵn;
c) Hàm số chẵn;
d) Hàm số không chẵn không lẻ.
3. Tìm giá trị lớn nhất, nhỏ nhất của hàm số :
.png)
ĐS:
a) – 4; 6;
b) – 3; $\sqrt{3}$ – 3