BÀI TẬP TRẮC NGHIỆM KHÁCH QUAN
Trong mỗi bài tập dưới đây, hãy chọn một phương án trong các phương án đã cho để được khẳng định đúng.
80. Hàm số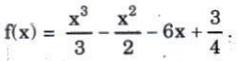 
A. Đồng biến trên khoảng (-2; 3).
B. Nghịch biến trên khoảng (-2; 3).
C. Nghịch biến trên khoảng .png)
D. Đồng biến trên khoảng .png)
Hướng dẫn giải
f'(x) = .png)
- x - 6 = 0 ⇔ x= -2; x = 3
f'(x) > 0 với .png)
, f'(x) < 0 với x .png)
(-2; 3).
Chọn B.
81. Hàm số .png)
A. Nghịch biến trên R.
B. Đồng biến trên khoảng .png)
và nghịch biến trên khoảng .png)
C. Đồng biến trên R.
D. Nghịch biến trên khoảng (0; 1).
Hướng dẫn giải
.png)
f'(x) = 0 chỉ tại x = 0 hoặc x = 1. Hàm số đồng biến trên R.
Chọn C.
82. Hàm số y = sinx - x
A. Đồng biến trên R.
B. Đồng biến trên khoảng .png)
C. Nghịch biến trên khoảng .png)
và đồng biến trên khoảng .png)
D. Nghịch biến trên R.
Hướng dẫn giải
.png)
Hàm số nghịch biến trên R.
Chọn D.
83. Hàm số .png)
A. Nhận điểm x = -1 làm điểm cực tiểu.
B. Nhận điểm x = 3 làm điểm cực đại.
C. Nhận điểm x = 1 làm điểm cực đại.
D. Nhận điểm x = 3 làm điểm cực tiểu.
Hướng dẫn giải
f'(x) = .png)
- 6x - 9 ⇔ x = -1 hoặc x = 3
f"(x) = 6x - 6
f"(-1) = -12 < 0 ⇒ f(x) nhận x = -1 làm điểm cực đại.
f"(3) = 12 > 0 ⇒ f(x) nhận x = 3 làm điểm cực tiểu.
Chọn D.
84. Hàm số .png)
A. Nhận điểm x = 3 làm điểm cực tiểu.
B. Nhận điểm x = 0 làm điểm cực đại.
C. Nhận điểm x = 3 làm điểm cực đại.
D. Nhận điểm x = 0 làm điểm cực tiểu.
Hướng dẫn giải
.png)
⇔ x = 0 hoặc x = 3
Hàm số liên tục trên R, y' chỉ đổi dấu một lần từ âm sang dương khi x đi qua x = 3. Hàm số nhận x = 3 làm điểm cực tiểu.
Chọn A.
85. Số điểm cực trị của hàm số .png)
là :
A. 0
B. 1
C. 3
D. 2.
Hướng dẫn giải
.png)
Hàm số có ba cực trị.
Chọn C.
86. Số điểm cực trị của hàm số .png)
là :
A. O
B. 2
C. 1
D. 3.
Hướng dẫn giải
.png)
⇔ x = -1 hoặc x = 3
Hàm số có hai cực trị.
Chọn B.
87. Hàm số f có đạo hàm là .png)
Số điểm cực trị của hàm số là :
A. 1
B. 2
C. 0
D. 3
Hướng dẫn giải
f'(x) = 0 ⇔ x = -1 hoặc x = 0 hoặc x = .png)
f'(x) = 0 tại ba điểm nhưng chỉ đổi dấu một lần khi x đi qua .png)
. Hàm số có một cực trị.
Chọn A.
88. Hàm số y = x - sin2x + 3
A. Nhận điểm .png)
làm điểm cực tiểu.
B. Nhận điểm .png)
làm điểm cực đại.
C. Nhận điểm làm điểm cực đại.
D. Nhận điểm .png)
làm điểm cực tiểu.
Hướng dẫn giải
y' = 1 – 2cosx = 0 ⇔ .png)
Hàm số đạt cực trị tại .png)
. Đạo hàm đổi dấu từ dương sang âm khi x đi qua .png)
. Hàm số nhận .png)
làm điểm cực đại.
Chọn C.
89. Giá trị lớn nhất của hàm số .png)
là :
A. -3
B. 1
C. -1
D. 0.
Hướng dẫn giải
.png)
Hàm số đồng biến trên .png)
Giá trị lớn nhất .png)
Chọn D.
90. Giá trị nhỏ nhất của hàm số y = 3sinx - 4cosx là :
A. 3
B. -5 .
C. -4
D. -3.
Hướng dẫn giải
.png)
Miny = -5.
Chọn B.
91. Giá trị lớn nhất của hàm số .png)
trên đoạn [-1; 2] là :
A. 6
B. 10
C. 15
D. 11.
Hướng dẫn giải
f'(x) = .png)
+ 6x – 12 = 0 ⇔ x = -2 hoặc x = 1
Max{f(-1), f(2), f(1)} = max{15; 6; -5} = 15 ⇒ .png)
Chọn C.
92. Giá trị lớn nhất của hàm số .png)
là :
A. 2
B. .png)
C. 0
D. 3.
Hướng dẫn giải
.png)
thuộc tập xác định.
⇒ .png)
Chọn A.
93. Gọi .png)
là đồ thị của hàm số .png)
A. Đường thẳng x = -1 là tiệm cận đứng của .
B. Đường thẳng y = 2x - 1 là tiệm cận xiên của .
C. Đường thẳng y = x + 1 là tiệm cận xiên của .
D. Đường thẳng y = x – 2 là tiệm cận xiên của .
Hướng dẫn giải
.png)
⇒ Tiệm cận đứng .png)
. Tiệm cận xiên y = x - 2.
Chọn D.
94. Gọi là đồ thị của hàm số .png)
A. Đường thẳng x = 1 là tiệm cận đứng của .
B. Đường thẳng .png)
là tiệm cận đứng của .
C. Đường thẳng y = 1 là tiệm cận ngang của .
D. Đường thẳng y = -x +1 là tiệm cận xiên của .
Hướng dẫn giải
.png)
⇒ Các tiệm cận đứng : x = .png)
, x = 3
.png)
⇒ tiệm cận ngang y =
Chọn B.
95. Gọi là đồ thị của hàm số .png)
A. Đường thẳng x = 2 là tiệm cận đứng của .
B. Đường thẳng y = x - 1 là tiệm cận xiên của .
C. Đường thẳng .png)
là tiệm cận ngang của .
D. Đường thẳng .png)
là tiệm cận ngang của .
Hướng dẫn giải
.png)
⇒ Tiệm cận đứng x = -1, x = .png)
.png)
⇒ Tiệm cận ngang y = .png)
Chọn C.
96. Đồ thị của hàm số .png)
A. cắt đường thẳng y = 1 tại hai điểm.
B. cắt đường thẳng y = 4 tại hai điểm.
C. tiếp xúc với đường thẳng y = 0.
D. không cắt đường thẳng y = -2.
Hướng dẫn giải
Phương trình hoành độ giao điểm của đường thẳng y = m và đồ thị hàm số là :
.png)
.png)
– 4(m + 1) = (m + 1)(m - 3) = 0 ⇔ m = -1 hoặc m = 3
• Nếu m < -1 hoặc m > 3 thì .png)
> 0. Phương trình (*) có hai nghiệm phân biệt. Đường thẳng y = m cắt đô thị tại hai điểm.
• Nếu m = -1 hoặc m = 3 thì = 0. Phương trình (*) có một nghiệm. Đường thẳng y = m tiếp xúc với đồ thị.
• Nếu -1 < m < 3 thì đường thẳng y = m không cắt đồ thị.
Chọn B.
97. Xét phương trình .png)
A. Với m = 5, phương trình đã cho có ba nghiệm.
B. Với m = -1, phương trình có hai nghiệm.
C. Với m = 4, phương trình có ba nghiệm phân biệt.
D. Với m = 2, phương trình có ba nghiệm phân biệt.
Hướng dẫn giải
Xét hàm số .png)
trên R.
y' = .png)
+ 6x = 0 ⇔ x = -2 hoặc x = 0
Bảng biến thiên:
.png)
Đồ thị hàm số .png)
cắt đường thẳng y = m tại ba điểm phân biệt nếu và chỉ nếu 0 < m < 4.
Chọn D.
.png)
98. Đồ thị hàm số .png)
A. Nhận điểm .png)
làm tâm đối xứng.
B. Nhận điểm .png)
làm tâm đối xứng.
C. Không có tâm đối xứng.
D. Nhận điểm .png)
làm tâm đối xứng.
Hướng dẫn giải
Hàm số .png)
có đồ thị là .png)
, có đường tiệm cận đứng là .png)
và tiệm cận ngang .png)
. Giao điểm của hai đường tiệm cận là .png)
là tâm đối xứng của .
Chọn A.
99. Số giao điểm của hai đường cong .png)
là :
A. 0
B.1
C. 3
D. 2.
Hướng dẫn giải
Phương trình hoành độ giao điểm của hai đường cong .png)
và .png)
là :
.png)
Số nghiệm của phương trình (*) bằng số giao điểm của hai đường cong.
Ta có :
.png)
⇔ x = -1; x = 1; x = 2
Vậy hai đường cong có 3 giao điểm.
Chọn C.
100. Các đồ thị của hai hàm số .png)
tiếp xúc với nhau tại điểm M có hoành độ là :
A. x = -1
B. x = 1
C. x = 2
D. .png)
.
Hướng dẫn giải
Hoành độ tiếp điểm của hai đường cong .png)
là nghiệm của hệ phương trình :
.png)
Chọn D.