Chương IV: SỐ PHỨC
§1. Số phức
TÓM TẮT LÍ THUYẾT
1. Định nghĩa
• Ta gọi là số phức, biểu thức có dạng a + bi với a, b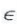 
R, .png)
= -1.
Tập hợp các số phức kí hiệu là C. Rõ ràng R .png)
C.
Với số phức z = a + bi thì a là phần thực của z, b là phần ảo của z, i là đơn vị ảo.
• Hai số phức .png)
bằng nhau khi và chỉ khi phần thực và phần ảo tương ứng bằng nhau.
.png)
⇔ a = c và b = d
• Trong hệ trục tọa độ vuông Oxy, số phức z = a + bi được biểu diễn bằng điểm M(a; b). Mặt phẳng tọa độ biểu diễn các số phức được gọi là mặt phẳng phức, trục Ox là trục thực, trục Oy là trục ảo.
.png)
• Môđun của số phức z = a + bi là số .png)
và kí hiệu là .png)
, là độ dài của vectơ .png)
với M(a; b) là điểm biểu diễn số phức z.
.png)
• Số phức liên hợp của số phức z = a + bi là số phức .png)
= a - bi. Trên mặt phẳng phức, hai số phức liên hợp được biểu diễn bằng các điểm đối xứng với nhau qua trục thực.
2. Các phép toán trên số phức
Cho các số phức .png)
= a + bi, .png)
= c + di
• Phép cộng: .png)
= (a + c) + (b + d)i
• Phép trừ: .png)
= (a - c) + (b - d)i
• Phép nhân : .png)
= (ac - bd) + (ad + bc)i
• Số nghịch đảo của số phức z khác 0, kí hiệu .png)
.png)
• Phép chia: Cho các số phức và , với khác 0.
Thương .png)
Các phép toán trên số phức có các tính chất giống như các phép toán tương ứng trong tập hợp số thực.