II. BÀI TẬP TRẮC NGHIỆM KHÁCH QUAN

Trong mỗi bài tập dưới đây, hãy chọn một phương án trong các phương án đã cho để được khẳng định đúng.

24. Hàm số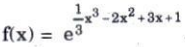

A. Đồng biến trên mỗi khoảng

B. Nghịch biến trên mỗi khoảng

C. Đồng biến trên khoảng và nghịch biến trên khoảng

D. Nghịch biến trên khoảng và đồng biến trên khoảng

Hướng dẫn giải

Xét sự biến thiên của hàm số ta thấy tập xác định của t(x) là D = R,

t'(x) = - 4x + 3 = 0 ⇔ x = 1 hoặc x = 3

Ta thấy hàm số t(x) nghịch biến trên khoảng (1; 3) và đồng biến trên các khoảng

Ta biết hàm số g(t) = có tập xác định là R, luôn đồng biến trên R, nghĩa là

Với mọi thuộc hoặc thuộc ta có thì

Suy ra

Điều đó có nghĩa là hàm số đồng biến trong các khoảng .

Chọn phương án A.

25. Hàm số f(x) = - 2sinx có giá trị nhỏ nhất là :

Hướng dẫn giải

Hàm số f(x) = - 2sinx liên tục trên R.

Đặt t = sinx ta có với mọi x R.

Xét hàm số g(t) = - 2t với t [-1; 1] ta có giá trị nhỏ nhất của g(t) trên [-1; 1] là giá trị nhỏ nhất của f(x) trên R.

g'(t) = 0 ⇔ t = 0 hoặc t = 2 (loại 2 [-1; 1])

= min{g(-1), g(1), g(0)} = min{3; -1; 0} = -1

Chọn phương án C.

26. Gọi là đồ thị của hàm số . Khi đó :

A. Đường thẳng y = x + 1 là tiệm cận xiên của khi x → .

B. Đường thẳng là tiệm cận xiên của khi x → .

C. Đường thẳng y = -x là tiệm cận xiên của khi x → .

D. Đồ thị không có tiệm cận xiên khi x → .

Hướng dẫn giải

Ta có:

Tiệm cận xiên của đồ thị hàm số khi x → là y = x +

Chọn B.

27. Đồ thị của hàm số y = − x + 1 tiếp xúc tại điểm (1; 1) với :

A. parabol y = 2 - 1

B. parabol y =

C. parabol y = - + 2x

D. đường thẳng y = 2x + 1.

Hướng dẫn giải

Điểm (1; 1) là điểm chung của các đồ thị các hàm số y = – x + 1 và y = 2 – 1; y = ; y = - + 2x.

Vì

nên chỉ các đồ thị của các hàm số y = − x + 1 và y = tiếp xúc tại điểm (1; 1).

Chọn B.

28. Cho hai số dương a và b. Đặt . Khi đó :

A. X > Y

B . X < Y

C. X Y

D. X Y.

Hướng dẫn giải

Theo bất đẳng thức Côsi, với mọi a > 0, b > 0 thì

Hàm số y = lnx đồng biến trên , do đó :

Chọn C.

29. Cho hai số không âm a và b. Đặt . Khi đó :

A. X>Y

B. X

C. XY

D. XY.

Hướng dẫn giải

Theo bất đẳng thức Côsi ta có với các số dương thì

Chọn D.

30. Cho là đồ thị của hàm số . Ta có thể suy ra đồ thị của hàm số bằng cách tịnh tiến theo vectơ .

A. = (3; 1)

B. = (3; -1)

C. = (-3; 1)

D. = (-3; -1).

Hướng dẫn giải

Ta có :

Tịnh tiến theo vectơ (-3; 0) ta được đồ thị

Tịnh tiến đồ thị theo vectơ (0; 1) ta được đồ thị hàm số

Vậy tịnh tiến theo vectơ = (-3; 0) + (0; 1) = (-3; 1) ta được đồ thị hàm số

Chọn C.

31. Cho hàm số . Khi đó :

Hướng dẫn giải

Chọn B.

32. Biết rằng đồ thị của hàm số y = và đồ thị của hàm số y = cắt nhau tại điểm . Khi đó :

A. a > 1 và b > 1

B. a> 1 và 0 < b <1

C. 0 < a < 1 và b > 1

D. 0 < a <1 và 0 < b <1.

Hướng dẫn giải

Đồ thị của hai hàm số y = và y = cắt nhau tại điểm tức là điểm thuộc cả hai đồ thị. Điều đó có nghĩa là

Đẳng thức (1) chứng tỏ >1 với x > 0 hay a > 1.

Đẳng thức (2) chứng tỏ > 0 với 0 < x < 1 hay 0 < b < 1.

Chọn B.

33. Cho hàm số . Khi đó :

Hướng dẫn giải

Chọn phương án A.

34. Đẳng thức : xảy ra nếu:

Hướng dẫn giải

Chọn D.

35. Gọi S là tập hợp tất cả các số nguyên dương k thỏa mãn điều kiện :

Khi đó :

A. S = {1}

B. S = {2}

C. S = {1;2}

D. S = Ø.

Hướng dẫn giải

• Với k = 1, I = -1 < e - 2

• Với k = 2, I = eln2 – (ln2 + 1) = (e - 1)ln2 - 1< e - 1 - 1 = e - 2

Chọn C.

36. Cho số phức z tùy ý. Xét các số phức Khi đó :

A. là số thực, là số thực.

B. là số thực, là số ảo.

C. là số ảo, là số thực.

D. là số ảo, là số ảo.

Hướng dẫn giải

Chọn A.

87. Cho số phức tùy ý z 1. Xét các số phức :

Khi đó :

A. là số thực, là số thực.

B. là số thực, là số ảo.

C. là số ảo, là số thực.

D. là số ảo, là số ảo.

Hướng dẫn giải

Chọn C.

38. Nếu mođun của số phức z bằng r (r > 0) thì modun của số phức bằng :

A. 4r

B. 2r

C.

D. r.

Hướng dẫn giải

Đặt thì

Chọn B.