CÂU HỎI VÀ BÀI TẬP
27. Hãy tìm dạng lượng giác của các số phức : $\bar{z}$; -z; $\large \frac{1}{\bar{z}}$; kz (k $\epsilon$ R*) trong mỗi trường hợp sau :
a) z = r(cos$\varphi$ + isin$\varphi$) (r > 0)
b) z = 1+ i$\sqrt{3}$.
Hướng dẫn giải
a) Ta có:
.png)
.png)
28. Viết các số phức sau dưới dạng lượng giác :
.png)
Hướng dẫn giải
.png)
.png)
29. Dùng công thức khai triển nhị thức Niutơn $(1+i)^{19}$ và công thức Moavrơ để tính : .png)
Hướng dẫn giải
Theo công thức nhị thức Niutơn:
.png)
30. Gọi M, M' là các điểm trong mặt phẳng phức theo thứ tự biểu diễn các số : z = 3 + i, z' = (3 - $\sqrt{3}$) + (1 +3$\sqrt{3}$)i.
a) Tính $\frac{z'}{z}$
b) Chứng minh rằng hiệu số acgumen của z' với acgumen của z là một số đo của góc lượng giác (OM, OM'). Tính số đo đó.
Hướng dẫn giải
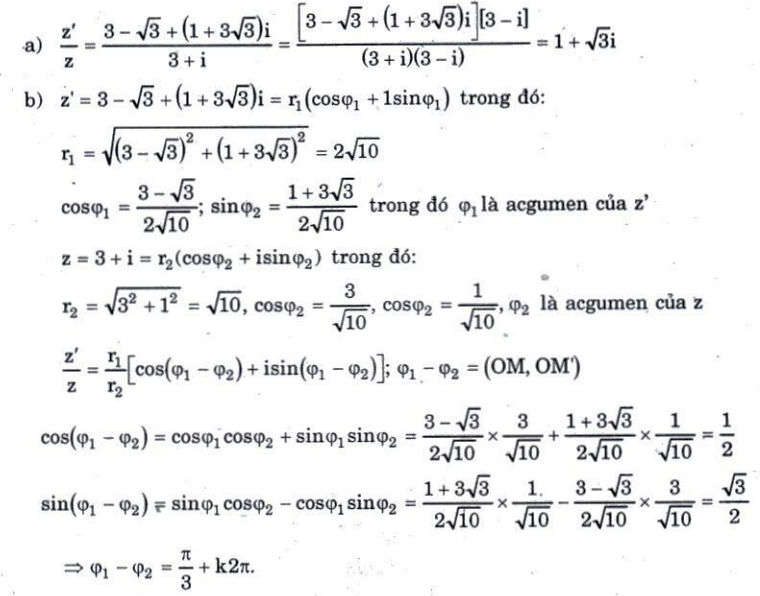
31. Cho các số phức .png)
a) Chứng minh rằng : .png)
là các nghiệm của phương trình .png)
b) Biểu diễn hình học các số phức .png)
Hướng dẫn giải
a) .png)
⇒ .png)
là nghiệm của phương trình
.png)
.png)
⇒ .png)
là nghiệm của phương trình
.png)
Vậy .png)
là nghiệm của phương trình
b) .png)
được biểu diễn bằng các đỉnh của tam giác đều ABC nội tiếp đường tròn tâm O bán kính đơn vị với .png)
.png)
.png)
32. Sử dụng công thức Moa-vrơ để tính sin4$\varphi$ và cos4$\varphi$ theo các lũy thừa của sin$\varphi$ và cos$\varphi$.
Hướng dẫn giải
.png)
33. Tính: .png)
Hướng dẫn giải
.png)
.png)
34. Cho số phức .png)
Tìm các số nguyên dương n để .png)
là số thực. Hỏi có chăng một số nguyên dương m để .png)
là số ảo ?
Hướng dẫn giải
.png)
a) là số thực khi n là số nguyên dương sao cho .png)
là bội của .png)
(để sin.png)
= 0). Điều này xảy ra khi n là bội của 3.
b) là số ảo khi m là số nguyên dương sao cho .png)
(để .png)
). Điều này xảy ra nếu có các số nguyên k và m sao cho .png)
⇔ 8m – 6k = 3. Không thể tìm được các cặp số nguyên như vậy, tức là không có số nguyên dương m để là số ảo.
35. Viết dạng lượng giác của số phức z và các căn bậc hai của z cho mỗi trường hợp sau :
a) |z| = 3 và một acgumen của iz là .png)
b) |z| = .png)
và một acgumen của .png)
Hướng dẫn giải
a) |z| = |iz| = 3. Đặt z = x + yi ⇒ iz = -y + xi
.png)
Dạng lượng giác của z là : .png)
Dạng lượng giác của các căn bậc hai của z là :
.png)
b) Ta có : .png)
Nếu một acgumen của z là $\varphi$ thì một acgumen của $\bar{z}$ là -$\varphi$.
Ta lại có .png)
tức là một acgumen của 1+ i là .png)
suy ra một acgumen của .png)
Theo giả thiết :
.png)
Dạng lượng giác của z là : .png)
Dạng lượng giác của các căn bậc hai của z là :
.png)
36. Viết dạng lượng giác của các số phức :
.png)
Hướng dẫn giải
.png)
Dạng lượng giác của số cần tìm là :
.png)
c) Ta có :
.png)
Nếu .png)
thì dạng lượng giác của 1 - cos$\varphi$ – isin$\varphi$ là biểu thức vế phải của (1). Nếu .png)
thì dạng lượng giác của số đã cho là :
.png)