Vấn đề 2. Xác định thiết diện tạo bởi một mặt phẳng với hình chóp.
1. Phương pháp
Để xác định thiết diện của hình chóp với một mặt phẳng, ta tìm giao tuyến của các mặt của hình chóp với mặt phẳng đó. Thông thường, ta áp dụng các định lí về quan hệ song song đã biết để xác định các giao tuyến ấy.
2. Ví dụ
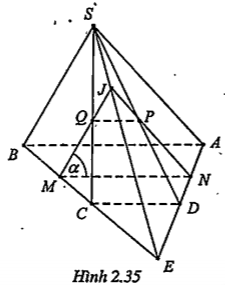
Ví dụ. Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). M là một điểm trên cạnh BC (không trùng với B và C). Mặt phẳng (\[\alpha \]) đi qua M và song song với mp (SAB).
a) Xác định thiết diện của hình chóp với mp(\[\alpha \]).
b) Gọi P, Q lần lượt là giao điểm của (\[\alpha \]) với SD và SC. Chứng minh rằng giao điểm J của NP, MQ chạy trên một đường thẳng cố định.
| Lời giải: a) Thiết diện của (\[\alpha \]) với hình chóp (\[\alpha \])//(SAB) Ta có: (ABCD)\[\cap \] (\[\alpha \])= MN (ABCD)\[\cap \] (SAB)= AB
\[\Rightarrow \]MN // AB (1) (\[\alpha \])//(SAB) (SAD)\[\cap \] (\[\alpha \])=PN (SAD)\[\cap \] (SAB)= SA \[\Rightarrow \]PN//SA CD//(\[\alpha \]) , (SCD)\[\supset \] CD (SCD) \[\cap \] (\[\alpha \])=PQ \[\Rightarrow \]PQ//CD (2) Mặt khác:AB//CD (3) (1),(2),(3)\[\Rightarrow \] MN // PQ Vậy thiết điện cần tìm là hình thang MNPQ. | Giải thích Áp dụng định lí 11.
|
| b) Chứng minh J chạy trên đường thẳng… Ta có: \[J\in PN,PN\subset \left( SAD \right)\Rightarrow J\in \left( SAD \right)\] \[J\in MQ,MQ\subset \left( SBC \right)\Rightarrow J\in \left( SBC \right)\] Do đó \[J\in \left( SAD \right)\cap \left( SBC \right)\] Mặt khác \[\left( SAD \right)\cap \left( SBC \right)=SE(E\in AD\cap BC)\] Suy ra \[J\in SE\] (cố định) Vậy khi M di động trên cạnh BC thì J chạy trên đoạn thẳng SE. | Vì (SAD) và (SBC) cố định nên giao tuyến SE của chúng cũng cố định. |