BÀI 3. ĐƯỜNG THẲNG VÀ MẶT PHẮNG SONG SONG
A. CÁC KIẾN THỨC CẦN NHỚ
I. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ MẶT PHẲNG
Trong không gian, đường thẳng d và mặt phẳng (\[\alpha \]) có ba vị trí tương đối sau:
| VỊ TRÍ TƯƠNG ĐỐI | SỐ ĐIỂM CHUNG | KÍ HIỆU |
| d cắt (\[\alpha \]) tại M | 1 | \[d\cap (\alpha )=M\] |
| d song song với (\[\alpha \]) | 0 | \[d//(\alpha )\] hoặc \[(\alpha )//d\] |
| d nằm trong (\[\alpha \]) | Vô số | \[d\subset (\alpha )\] |
II. ĐỊNH NGHĨA: Một đường thẳng và một mặt phẳng được gọi là song song nếu chúng không có điểm chung
\[d//(\alpha )\Leftrightarrow d\cap (\alpha )=\varnothing \]
II. CÁC ĐỊNH LÍ VÀ TÍNH CHẤT
1. Định lý 4: Nếu một đường thẳng d không nằm trên mp(\[\alpha \]) và song song với một đường thẳng a trong (\[\alpha \]) thì d song song với (\[\alpha \]).
\[d\not\subset (\alpha ),a\subset (\alpha ),d//a\Rightarrow d//(\alpha )\]
Chú ý quan trọng:
• Định lý 4 dùng để chứng minh một đường thẳng song song với một mặt phẳng.
• Khi một đường thẳng song song với một mặt phẳng thì nó không song song với mọi đường thẳng trong mặt phẳng ấy.
2. Định lý 5: Cho đường thẳng d song song với mp (\[\alpha \]). Nếu mp(\[\beta \]) đi qua d và cắt mp (\[\alpha \]) thì giao tuyến x của (\[\alpha \]) và (\[\beta \]) song song với d.
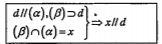
Chú ý: Định lý 5 có thể dùng để chứng minh hai đường thẳng song song.
3. Định lý 6: Nếu hai mặt phẳng cắt nhau và cùng song song với một đường thẳng thì giao tuyến của chúng song song với đường thẳng đó.
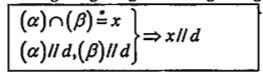
Chú ý. Định lý 6 có thể dùng để chứng minh hai đường thẳng song song.
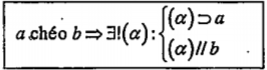
4. Định lý 7: Cho a và b là hai đường thẳng chéo nhau. Khi đó có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.