CÂU HỎI VÀ BÀI TẬP ÔN CHƯƠNG 2
Bài 2.37. Trong mặt phẳng (\[\alpha \]) cho tam giác ABC. Từ ba đỉnh của tam giác này ta vẽ ba nửa đường thẳng song song cùng chiều Ax, By, Cz không nằm trong (\[\alpha \]). Trên Ax lấy đoạn AA' =a, trên By lấy đoạn BB' = b, trên Cz lấy đoạn CC' = c.
a) Gọi I, J, K lần lượt là các giao điểm B'C', C'A' và A'B' với (\[\alpha \]).
Chứng minh rằng \[\frac{IB}{IC}.\frac{JC}{JA}.\frac{KA}{KB}=1\]
b) Gọi G và G’ lần lượt là trọng tâm của các tam giác ABC và A'B’C’.
Chứng minh: GG’//AA'.
c) Tính GG' theo a, b, c.
| a) Chứng minh \[\frac{IB}{IC}.\frac{JC}{JA}.\frac{KA}{KB}=1\] Ta có: \[BB'//CC'\Rightarrow \frac{IB}{IC}=\frac{BB'}{CC'}\Rightarrow \frac{IB}{IC}=\frac{b}{c}\] | Giải thích • Ta thấy I, J, K là điểm chung của hai mặt phẳng phân biệt (ABC) và (A'B'C’) nên chúng lần lượt là giao điểm của B’C’, C’A' và A'B' với BC, CA và AB. |
| \[AA'//CC'\Rightarrow \frac{JC}{IA}=\frac{CC'}{AA'}\Rightarrow \frac{JC}{IA}=\frac{c}{a}\] \[AA'//BB'\Rightarrow \frac{KA}{KB}=\frac{A{A}'}{B{B}'}\Rightarrow \frac{KA}{KB}=\frac{a}{b}\] Suy ra \[\frac{IB}{IC}.\frac{JC}{J\text{A}}.\frac{K\text{A}}{KB}=\frac{b}{c}.\frac{c}{a}.\frac{a}{b}=1\] | • Áp dụng định lí Thales vào các tam giác ICC’, JCC’, KBB' ta sẽ được các tỉ lệ thức của bài làm.
|
| b) Chứng minh GG'//AA' Ta có: EE’ là đường trung bình của hình thang ABB’A' nên: EE' // AA', AA'//CC \[\Rightarrow \]EE’//CC’ (1) Mặt khác: \[\frac{E'G'}{EC'}=\frac{1}{3},\frac{EG}{EC}=\frac{1}{3}\Rightarrow \frac{E'G'}{EC'}=\frac{EG}{EC}\] (2) (1) và (2)\[\Rightarrow GG'//\text{EE }\!\!'\!\!\text{ //CC }\!\!'\!\!\text{ }\] Vậy GG’//AA’ |
|
| c) Tính GG’ Gọi \[F\cap GG'\cap CE'\], ta có: • \[\Delta E'CC':\frac{E'G'}{E'C'}=\frac{G'F}{CC'}\] \[\Rightarrow G'F=\frac{E'G'}{E'C'}.CC'\Rightarrow G'F=\frac{1}{3}c\] (1) • \[\Delta CEE':\frac{CG}{CE}=\frac{GF}{EE'}\] \[\Rightarrow FG=\frac{CG}{CE}.EE'\Rightarrow FG=\frac{2}{3}EE'\] mà \[EE'=\frac{AA'+BB'}{2}\Rightarrow EE'=\frac{a+b}{2}\] nên \[FG=\frac{2}{3}.\frac{a+b}{2}=\frac{1}{3}\left( a+b \right)\] (2) Ta có: \[G{G}'={G}'F+FG=\frac{1}{3}c+\frac{1}{3}\left( b+a \right)\] Vậy \[G{G}'=\frac{1}{3}\left( a+b+c \right)\] | Để ý rằng: • Trong tam giác E’CC' có FG’//CC'. • Trong tam giác CEE’ có FG //EE’ • Đường trung bình EE’ của hình thang ABB’A' bằng nửa tổng độ dài hai đáy. |
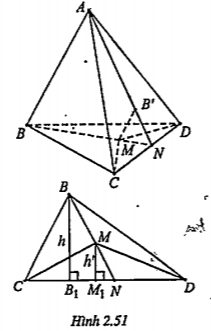
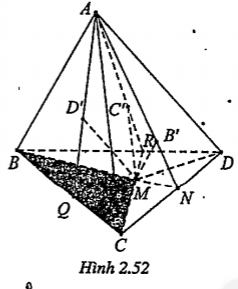
Bài 2.38. Cho tứ diện ABCD và điểm M nằm trong tam giác BCD.
a) Dựng đường thẳng qua M và song song với hai mặt phẳng (ABC) và (ABD). Giả sử đường thẳng này cắt mặt phẳng (ACD) tại B’. Chứng
minh rằng AB’, BM và CD đồng quy tại một điểm.
b) Chứng minh \[\frac{MB'}{BA}=\frac{dt\left( \Delta MCD \right)}{dt\left( \Delta BCD \right)}\]
c) Đường thẳng song song với hai mặt phẳng (ACB) và (ACD) kẻ từ M cắt (ABD) tại C’ và đường thẳng song song với hai mặt phẳng (ADC) và (ADB) kẻ từ M cắt (ABC) tại D’. Chứng minh rằng
\[\frac{M{B}'}{BA}+\frac{M{C}'}{CA}+\frac{M{D}'}{DA}=1\]
| Lời giải a) Chứng minh AB’,BM và CD đồng quy Đường thẳng d qua M và d//(ABC), d//(ABD) nên d//AB (giao tuyến của (ABC) và (ABD)). \[\Rightarrow \exists (d,AB)\cap (ACD)=AB'\] Gọi \[N\in BM\cap CD\]. Ta có: \[\Rightarrow N\in (d,AB)\cap (ACD)\Rightarrow N\in AB'\] Vậy AB',BM và CD đồng quy tại N.
| Giải thích Hướng dẫn: • Áp dụng định lí 6, bài3, ta có d//AB. • Gọi N là giao điểm của BM và CD, ta chứng minh N thuộc AB’.
|
| b) Chứng minh \[\frac{MB'}{BA}=\frac{dt\left( \Delta MCD \right)}{dt\left( \Delta BCD \right)}\] Ta có: MB’//AB nên \[\frac{NM}{NB}=\frac{MB'}{BA}\] (*) | Xem hình 2.51 để thấy được sự liên hệ giữa tỉ số diện tích của hai tam giác BCD và MCD (có chung cạnh CD).
|
| Mặt khác: \[dt(\Delta BCD)=\frac{1}{2}CD.h\] (1) (h= BB1 :đường cao \[\Delta \]BCD) \[dt(\Delta MCD)=\frac{1}{2}CD.h'\] (2) (h’= MM1 :đường cao \[\Delta \]MCD) (1) và (2) \[\Delta NB{{B}_{1}}\] có \[M{{M}_{1}}//B{{B}_{1}}\] Nên \[\frac{NM}{NB}=\frac{h}{h'}\] (4) (3) và (4) (*) và (*’)\[\Rightarrow \frac{MB'}{BA}=\frac{dt\left( \text{ }\!\!\Delta\!\!\text{ }MC\text{D} \right)}{dt\left( \text{ }\!\!\Delta\!\!\text{ }BC\text{D} \right)}\] |
|
| c) Chứng minh \[\frac{M{B}'}{BA}+\frac{M{C}'}{CA}+\frac{M{D}'}{DA}=1\] Ta có: \[\frac{M{B}'}{BA}=\frac{dt\left( \text{ }\!\!\Delta\!\!\text{ }MC\text{D} \right)}{dt\left( \text{ }\!\!\Delta\!\!\text{ }BC\text{D} \right)}\] Tương tự: \[\frac{MC'}{CA}=\frac{dt\left( \text{ }\!\!\Delta\!\!\text{ }MB\text{D} \right)}{dt\left( \text{ }\!\!\Delta\!\!\text{ }BC\text{D} \right)}\] \[\frac{MD'}{DA}=\frac{dt\left( \text{ }\!\!\Delta\!\!\text{ }MB\text{C} \right)}{dt\left( \text{ }\!\!\Delta\!\!\text{ }BC\text{D} \right)}\] ⇒ \[\frac{M{B}'}{BA}+\frac{M{C}'}{CA}+\frac{M{D}'}{DA}=\frac{dt\left( \text{ }\!\!\Delta\!\!\text{ }MC\text{D} \right)}{dt\left( \text{ }\!\!\Delta\!\!\text{ }BC\text{D} \right)}+\] \[\frac{dt\left( \text{ }\!\!\Delta\!\!\text{ }MB\text{D} \right)}{dt\left( \text{ }\!\!\Delta\!\!\text{ }BC\text{D} \right)}+\frac{dt\left( \text{ }\!\!\Delta\!\!\text{ }MBC \right)}{dt\left( \text{ }\!\!\Delta\!\!\text{ }BC\text{D} \right)}=\] \[=\frac{dt\left( \text{ }\!\!\Delta\!\!\text{ BCD} \right)}{dt\left( \text{ }\!\!\Delta\!\!\text{ }BC\text{D} \right)}=1\] | Áp dụng kết quả của câu a) và câu b) ta suy ra điều phải chứng minh.
|
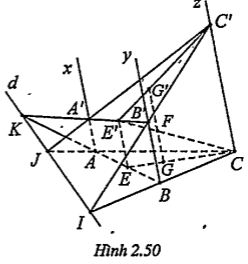
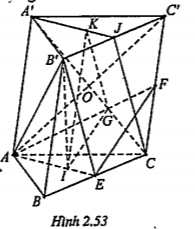
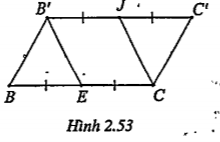
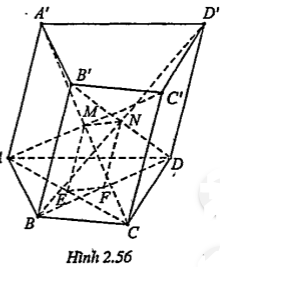
Bài 2.39. Từ các đỉnh của tam giác ABC ta kẻ các đoạn thẳng AA', BB’, CC’ song song cùng chiều, bằng nhau và không nằm trong mặt phẳng của tam giác. Gọi I, G và K lần lượt là trọng tâm của các tam giác ABC, ACC’ và A'B’C’.
a) Chứng minh (IGK)//(BB’C’C).
b) Chứng minh rằng (A'GK)//(AIB’).
| Lời giải a) Chứng minh (IJK)//(BB’C’C) Gọi E, F, J lần lượt là trung điểm lần của các cạnh BC,CC’ và B’C’. Ta có: EI//AA' (1)
(1) và (2) \[\Rightarrow IK//AA'\Rightarrow IK//BB'\] (3)
\[\Rightarrow I//EF\subset \left( BB'C'C \right)\] (4) (3) và (4)\[\Rightarrow \](IGK)//(BB’C’C) | Giải thích Vì E, F, J lần lượt là trung điểm của BC, CC’, B’C’ nên I, G, K lần lược nằm trên các trung tuyến AE, AF và A'J. Nhắc lại: Để chứng minh hai mặt phẳng song song ta chứng minh trong mặt này có hai đường thẳng cắt nhau song song với hai đường thẳng của mặt phẳng kia.
|
| b) Chứng minh (A’GK)//(AIB’) Gọi O là tâm của hình bình hành ACC'A' thì \[G\in CA'\]. Khi đó:(A’GK)=(A’CJ). Ta cũng có (AIB')\[\equiv \] (AEB’). Xét hai mặt phẳng (A'CJ) và (AEB’) có:
| Hình bình hành BB'C'C có J, E là trung điểm của B’C’ và BC nên ta dễ dàng chứng minh được JC//EB’.
|
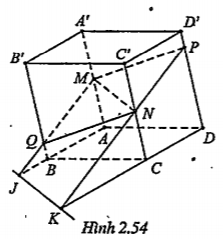
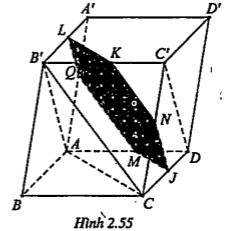
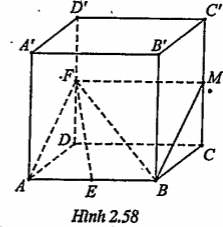
Bài 2.40. Cho hình hộp ABCD.A'B'C'D'. Gọi M và N lần lượt là trung điểm của hai cạnh bên AA' và CC'. Một điểm P nằm trên cạnh bên DD'.
a) Xác định giao điểm Q của đường thẳng BB' với mặt phẳng (MNP).
b) Mặt phẳng (MNP) cắt hình hộp theo một thiết diện. Thiết diện đó có tính chất gì?
c) Tìm giao tuyến của mặt phẳng (MNP) với mặt phẳng (ABCD) của hình hộp.
| a) Xác định Q Ta có: \[\Rightarrow \left( MNP \right)\cap \left( AA',BB' \right)=MQ//NP\] |
|
| b)Tính chất của tứ giác MPNQ Ta có: NP//MQ, MP//NQ \[\Rightarrow \]MPNQ là hình bình hành. |
|
| c) Giao tuyến của (MNP) với (ABCD) Gọi \[J\in MQ\cap AB,K\in PN\cap CD\], ta có: \[J\in MQ\Rightarrow J\in \left( MNP \right)\] \[J\in AB\Rightarrow J\in \left( ABCD \right)\] \[\Rightarrow J\in \left( MNP \right)\cap \left( ABCD \right)\] Tương tự, \[K\in \left( MNP \right)\cap \left( ABCD \right)\] Vậy \[\left( MNP \right)\cap \left( ABCD \right)=JK\]. Chú ý. Nếu P là trung điểm của DD’ thì mặt phẳng (MNP) không cắt mặt phẳng (ABCD). | Cần chú ý rằng (MNP) chính là mặt phẳng (MPNQ). |
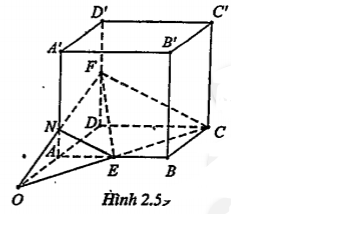
Bài 2.41.Cho hình hộp ABCD.A’B’C’D’. Hai điểm M và N lần lượt nằm trên hai cạnh AD và CC’ sao cho \[\frac{AM}{M\text{D}}=\frac{CN}{N{C}'}\]
a) Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACB’)
b) Xác định thiết diện của hình chóp cắt bởi mặt phẳng đi qua MN và song song với mặt phẳng (ACB’)
| Lời giải a) Chứng minh MN//(ACB’) Vē MJ//AC (J\[\in \]CD), ta có: \[\frac{CJ}{\text{JD}}=\frac{AM}{\text{MD}}=\frac{CN}{N{C}'}\]\[\Rightarrow \frac{CJ}{\text{JD}}=\frac{CN}{N{C}'}\] \[\Rightarrow JN//C'D\] Mặt khác C’D//AB’ nên JN//AB’. Xét hai mặt phẳng (ACB’) và (MNJ) có:
\[\Rightarrow MN//\left( ACB' \right)\] | Giải thích Để chứng minh một đường thẳng song song với mặt phẳng, ta có thể chứng minh đường thẳng đó nằm trong mặt phẳng song song với mặt phẳng đã cho. Từ giả thiết \[\frac{AM}{M\text{D}}=\frac{CN}{N{C}'}\] gợi ý cho ta vẽ thêm MJ// AC để tạo ra mặt phẳng (MNJ).
|
| b) Xác định thiết diện... Gọi (\[\alpha \]) là mặt phẳng qua MN và song Song với mặt phẳng (ACB’) Ta có: \[\left( \alpha \right)\cap \left( ABCD \right)=MJ//AC\] \[\left( \alpha \right)\cap \left( CDD'C' \right)=JN//DC'\] \[\left( \alpha \right)\cap \left( BCC'B' \right)=NK//B'C'(K\in B'C')\] \[\left( \alpha \right)\cap \left( A'B'C'D' \right)=KL//MJ(L\in A'B')\] \[\left( \alpha \right)\cap \left( AA'B'B \right)=LQ//AB'(Q\in AA')\] \[\left( \alpha \right)\cap \left( AA'DD' \right)=MQ\] Vậy thiết diện cần tìm là lục giác MJNKLQ. | Ta tìm các đoạn giao tuyến nối tiếp nhau của (\[\alpha \]) cắt bởi các mặt của hình hộp đã cho. Vì (\[\alpha \]) qua MN và song song với (ACB’) nên các cạnh đối diện của lục giác MJNKLQ song song với nhau. |
Bài 2.42. Cho hình lăng trụ tứ giác ABCD.A’B’C’D’.
a) Chứng minh rằng hai đường chéo AC’ và A’C cắt nhau tại M và hai đường chéo BD’ và B’D cắt nhau tại N.
b) Cho E và F lần lượt là trung điểm của hai đường chéo AC và BD.Chứng minh MN = EF.
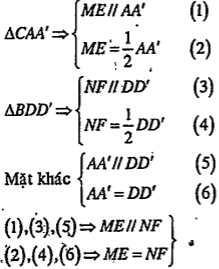
| Lời giải a) Chứng minh AC' cắt A'C, BD' cắt B'D Tứ giác ACC’A' là hình bình hành nên hai đường chéo AC’ và CA’ cắt nhau tại trung điểm I của mỗi đường Tứ giác BDD'B' là hình bình hành nên hai đường chéo BD’ và DB’ cắt nhau tại trung điểm J của mỗi đường | Giải thích Vì các cạnh bên của hình lăng trụ đều song song và bằng nhau nên các mặt ACC'A' và BDD’B' đều là những hình bình hành. |
| b) Chứng minh MN = EF
\[\Rightarrow \]MNFE là hình bình hành \[\Rightarrow \]MN=EF. | Ta chứng minh tứ giác MNFE là hình bình hành. Để ý rằng ME, NF lần lượt là đường trung bình của các tam giác CAA' và BDD’
|
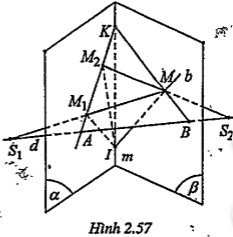
Bài 2.43. Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt (α) ở A và cắt (β) ở B ta lấy hai diểm cố định S1, S2 không thuộc (α), (β). Gọi M là một điểm di động trên (β). Giả sử các đường thẳng MS1, MS2 cắt (α) lần lượt tại M1 và M2.
a) Chứng minh rằng M1M2 luôn luôn đi qua một điểm cố định.
b) Giả sử đường thẳng M1M2 cắt giao tuyến m tại K. Chứng minh rằng ba điểm K, B, M thẳng hàng.
c) Gọi b là một đường thẳng thuộc mặt phẳng (β) nhưng không đi qua điểm B và cắt m tại I. Chứng minh rằng khi M di động trên b thì các điểm M1 và M2 di động trên hai đường thẳng cố định thuộc mặt phẳng (α).
| Lời giải a) Chứng minh M1M2 đi qua A Vì M\[\in d\] nên tồn tại mặt phẳng (M,d). Mặt phẳng này chứa MS1, MS2 và điểm A. (M,d)\[\cap \] (α)= M1M2 Mặt khác: \[A\in \] (M,d)\[\cap \] (α)
Vậy M1M2 đi qua điểm cố định A. | Giải thích Ta chứng minh A, M1 và M2 cùng thuộc giao tuyến của hai mặt phẳng phân biệt. |
| b) Chứng minh K,M,B thẳng hàng Ta có: \[K\in m\cap {{M}_{1}}{{M}_{2}}\Rightarrow K\in \left( \beta \right)\cap \left( M,d \right)\] \[M\in \left( \beta \right)\cap {{S}_{2}}{{M}_{2}}\Rightarrow M\in \left( \beta \right)\cap \left( M,d \right)\] \[B\in \left( \beta \right)\cap d\Rightarrow B\in \left( \beta \right)\cap \left( M,d \right)\] Vậy K,M,B thẳng hàng vì chúng cùng nằm trên giao tuyến của hai mặt phẳng (\[\beta \]) và (M,d).
| Ta chứng minh ba điểm K, M, B cùng thuộc giao tuyến của hai mặt phẳng phân biệt.
|
| c) Chứng minh M1, M2.. Ta có: \[I\in b\cap m\Rightarrow I\in \left( \alpha \right)\cap \left( {{S}_{1}},b \right)\] \[{{M}_{1}}\in \left( \alpha \right)\cap {{S}_{1}}M\Rightarrow {{M}_{1}}\in \left( \alpha \right)\cap \left( {{S}_{1}},b \right)\] \[\Rightarrow I{{M}_{1}}=\left( \alpha \right)\cap \left( {{S}_{1}},b \right)\] M1 chạy trên IM1 cố định. Tương tự \[I{{M}_{2}}=\left( \alpha \right)\cap \left( {{S}_{2}},b \right)\], nên M2 chạy trên IM2 cố định.
|
|
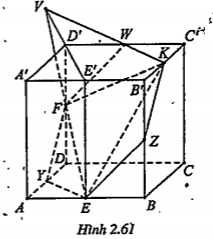
Bài 2.44. Cho hình lập phương ABCD.A'B’C’D’ và các trung điểm E, F của các cạnh AB, DD'. Hãy xác định thiết diện của hình lập phương cắt bởi các mặt phẳng (EFB), (EFC), (EFC’) và (EFK) với K là trung điểm của cạnh B’C’.
| Lời giải Thiết diện của hình lập phương với (EFB) Ta có: (EFB)\[\cap \] (ADD'A') = AF (EFB)\[\cap \] (CDD'C’)= FM//CD (M\[\in \]CC’) (EFB)\[\cap \] (BCC'B')=BM. Vậy thiết diện cần tìm là tứ giác ABMF. | Giải thích Cần chú ý rằng (EFB) = (AFB).
|
| Thiết diện của hình lập phương với (EFC). (EFC)\[\cap \] (ABCD)=CE (EFC)\[\cap \] (CDD'C')=CF Trong (ABCD), gọi O\[\in \]CE\[\cap \]AD. Trong (ADD'A'), gọi N\[\in \]FO\[\cap \]AA'. Khi đó: (EFC)\[\cap \] (ADD'A')= FN. Vậy thiết diện cần tìm là tứ giác CENF | Cần tìm giao điểm của AA’ với mặt với (EFC)
|
| • Thiết diện của hình lập phương với (EFC’) Trong (CDD’C’), gọi P\[\in \]CD\[\cap \]C'F. Trong(ABCD), gọi R\[\in \]AD\[\cap \]PE. Trong (BCC'B'), gọi Q\[\in \]BB'\[\cap \]TC’. Khi đó mặt phẳng (EFC’) cắt các mặt (CDD'C'), (ADD'A'), (ABCD), (ABB'A'), (BCC'B') lần lượt theo các đoạn giao tuyến C’F, FR, RE, EQ và QC’. Vậy thiết diện cần tìm là ngũ giác C’FREQ. | Trước hết, ta thấy (EFC'), cắt mặt phẳng (CDD’C’) theo giao tuyến C’F (gọi là giao tuyến gốc). Từ giao tuyến gốc này, ta tìm giao điểm của nó với một số cạnh của hình hộp sẽ được các đoạn giao tuyến còn lại.
|
| • Thiết diện của hình lập phương với (EFK) Gọi E là trung điểm của A’B’. Trong (DD’,EE’), gọi V\[\in \]D'E’\[\cap \]EF. Trong (A'B'C'D'), gọi W\[\in \]C'D’\[\cap \]VK. Khi đó: (EFK)\[\cap \] (A'B'C'D') = KW (EFK)\[\cap \] (CDD'C')=FW (EFK)\[\cap \] (ABCD)=EY // KW (Y\[\in \]AD) (EFK) n(ADDYA')=FY (EFK)\[\cap \] (ABB’A')=EZ//FW (Z\[\in \]BB’) (EFK)\[\cap \] (BCC’B’)=KZ// FY. Vậy thiết diện cần tìm là lục giác đều KWFYEZ. | Chú ý. • Vì EE//DD’ nên tồn tại duy nhất mặt phẳng (DD’, EE’). Trong mặt phẳng này ta thấy E’D’ cắt EF. Nhờ đó ta tạo được “giao tuyến gốc" là VK. • Các mặt đối diện của hình lập phương song song với nhau nên các đoạn giao tuyến của các mặt này với mặt phẳng (EFK) cũng song song với nhau và bằng nửa đường chéo hình vuông có cạnh là cạnh của hình lập phương. Vì vậy thiết diện thu được là một hình lục giác đều.
|

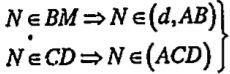
.png) (3)
(3).png) (*')
(*')
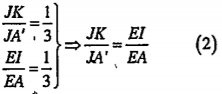
.png)
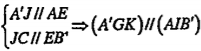
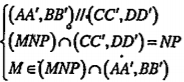
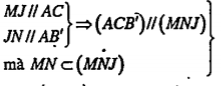
.png)