B. DẠNG TOÁN CƠ BẢN
Vấn đề 1: Chứng minh đường thẳng song song với mặt phẳng
1. Phương pháp
Dùng định lí 4:
Nếu một đường thẳng d không nằm trên mp(\[\alpha \]) và song song với một đường thẳng a trong (\[\alpha \]) thì d song song với (\[\alpha \]).
2. Ví dụ.
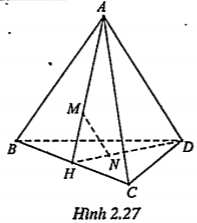
Ví dụ. Cho tứ diện ABCD. Gọi M, N lần lượt là trọng tâm của tam giác ABC và BCD. Chứng minh rằng MN//(ABD) và MN//(ACD).
| Lời giải Gọi H là trung điểm của BC, ta có
\[M\in AH,N\in DH\] \[\frac{HM}{HA}=\frac{HN}{HD}=\frac{1}{3}\Rightarrow MN//AD\] Như vậy: \[MN//AD,AD\subset (ABD)\Rightarrow MN//(ABD)\] \[MN//AD,AD\subset (ACD)\Rightarrow MN//(ACD)\] | Hướng dẫn
|