BÀI 4. HAI MẶT PHẲNG SONG SONG
A. CÁC KIẾN THỨC CẦN NHỚ
I. ĐỊNH NGHĨA
Hai mặt phẳng được gọi là song song nếu chúng không có điểm chung.
\[\left( \alpha \right)//\left( \beta \right)\Leftrightarrow \left( \alpha \right)\cap \left( \beta \right)=\varnothing \]
II. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI MẶT PHẲNG
Trong không gian, hai mặt phẳng \[\left( \alpha \right)\] và \[\left( \beta \right)\]có 3 vị trí tương đối sau đây:
1) \[\left( \alpha \right)//\left( \beta \right)\Leftrightarrow \left( \alpha \right)\cap \left( \beta \right)=\varnothing \]
2) \[\left( \alpha \right)\] cắt \[\left( \beta \right)\Leftrightarrow \left( \alpha \right)\cap \left( \beta \right)=\varnothing \]
3) \[\left( \alpha \right)\equiv \left( \beta \right)\Leftrightarrow \left( \alpha \right)\cap \left( \beta \right)=\left( \alpha \right)\] hoặc \[\left( \beta \right)\]
III. CÁC TÍNH CHẤT:
1. Định lí 8. Nếu hai mp\[\left( \alpha \right)\] và \[\left( \beta \right)\] song song với nhau thì mọi đường thẳng a nằm trong \[\left( \alpha \right)\] đều song song với \[\left( \beta \right)\]
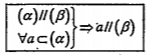
2. Định lý 9. (Điều kiện song song của hai mp); Nếu mp\[\left( \alpha \right)\] chứa hai đường thẳng a, b cắt nhau và hai đường thẳng này cùng song song với một mp\[\left( \beta \right)\] cho trước thì hai mp\[\left( \alpha \right)\] và \[\left( \beta \right)\] song song với nhau.
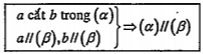
Hệ quả. Nếu mp\[\left( \alpha \right)\] chứa hai đường thẳng a, b cắt nhau và hai đường thẳng này cùng song song với hai đường thẳng a’ và b’ ở trong \[\left( \beta \right)\] thì hai mp\[\left( \alpha \right)\] và \[\left( \beta \right)\] song song với nhau.
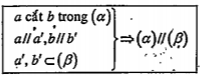
Chú ý. Dùng định lý 9 hoặc hệ qủa của nó để chứng minh hai mp song song
3. Định lý 10. Qua điểm A cho trước không nằm trên mp\[\left( \alpha \right)\] cho trước có một và chỉ một mp\[\left( \beta \right)\] song song với mp\[\left( \alpha \right)\].
\[A\notin \left( \alpha \right)\Rightarrow \exists mp\left( \beta \right)//\left( \alpha \right)\]
a) Hệ qủa 1
\[a//\left( \alpha \right)\Rightarrow \exists mp\left( \beta \right):\left( \beta \right)//\left( \alpha \right)\] và \[\left( \beta \right)\supset a\]
b) Hệ qủa 2
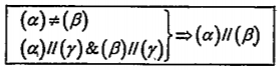
c) Hệ quả 3
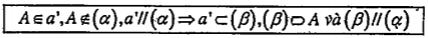
Chú ý. Có thể dùng định lý 10, hệ qủa 1 và 2 để chứng minh hai mp song song
4. Định lý 11. Nếu hai mp\[\left( \alpha \right)\] và \[\left( \beta \right)\] song song thì mọi mp \[\left( \gamma \right)\] đã cắt \[\left( \alpha \right)\] đều phải cắt \[\left( \beta \right)\]và các giao tuyến của chúng song song.
Chú ý. Có thể dùng định lý 11 để chứng minh hai đường thẳng song song hoặc tìm thiết diện của một mặt phẳng song song với một mp cho trước.
IV. ĐỊNH LÍ THALES
Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
V. HÌNH LĂNG TRỤ
Định nghĩa: Hình hợp bởi các hình bình hành A1A2A2’A1’, A2A3A3'A1',...,AnA1An’A1’ và hai miền đa giác A1A2...An , A1’A2’…An’ nằm trong hai mp song song được gọi là hình lăng trụ (hay lăng trụ).
• Các hình bình hành A1A2A2’A1’, A2A3A3'A1',...,AnA1An’ là các mặt bên
• Hai miền đa giác A1A2...An , A1’A2’…An’ là hai mặt đáy.
• Các đoạn thẳng A1A1', .., AnAn' là các cạnh bên
• Các đoạn thẳng A1A2 ...A1'A2' là các cạnh đáy.
• Ký hiệu lăng trụ: A1A2...An , A1’A2’…An’
• Gọi tên lăng trụ theo tên của đa giác đáy: Lăng trụ tam giác (có đáy là tam giác), lăng trụ tứ giác (có đáy là tứ giác),...
VI. HÌNH CHÓP CỤT
Định nghĩa: Cho hình chóp S.A1A2...An. Một mặt phẳng không qua đỉnh, song song với mặt phẳng đáy của hình chóp cắt các cạnh SA1, SA2 ..., SAn lần lượt tại A1’A2’…An’. Hình tạo bởi thiết diện A1’A2’…An’ và đáy A1A2...An của hình chóp cùng với các tứ giác A1’A2’A2A1, A’2A’3A3A2,…,A’nA'1A1An gọi là hình chóp cụt, kí hiệu là A1’A2’…An’ , A1A2...An .
