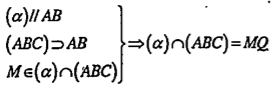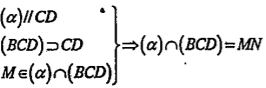Vấn đề 2. Dựng thiết diện song song với một đường thẳng
1. Phương pháp
Ta có thể sử dụng định lí 5:
Cho đường thẳng d song song với mp(\[\alpha \]). Nếu mp(\[\beta \]) đi qua d và cắt mp(\[\alpha \]) thì giao tuyến x của (\[\alpha \]) và (\[\beta \]) song song với d.
2. Ví dụ
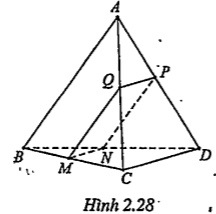
Ví dụ. Cho tứ diện ABCD. Gọi M là một điểm bất kỳ trên cạnh BC, (\[\alpha \]) là mặt phẳng qua M và song song với AB và CD. Xác định thiết diện của (\[\alpha \]) với tứ diện đã cho. Thiết diện là hình gì?
| Lời giải
sao cho MQ//AB(\[Q\in AC\])
Sao cho MN//CD(\[N\in BD\]) Tương tự, ta có \[\left( \alpha \right)\cap \left( ABD \right)=NP//AB\]\[\left( P\in AD \right)\] và \[\left( \alpha \right)\cap \left( ACD \right)=PQ//CD\]
Thiết diện cần tìm là tứ giác MNPQ. Mặt khác: \[MN//PQ(//CD)\] \[MQ//NP(//AB)\] Vậy MNPQ là hình bình hành. | Hướng dẫn
|