Vấn đề 2. Dùng phép đối xứng tâm để tìm tập hợp điểm
1. Phương pháp
a. Để tìm tập hợp điểm M’, ta làm như sau:
• Xác định phép đối xứng trục biến M thành M'.
• Tìm tập hợp của M.
• Suy ra tập hợp của M’.
2. Ví dụ
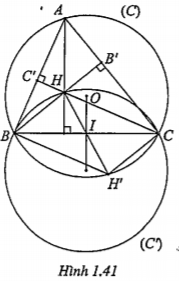
Ví dụ. Cho trên đường tròn (C) tâm O hai điểm cố định B, C và một điểm A thay đổi. Gọi H là trực tâm của tam giác ABC và H’ là điểm sao cho tứ giác BHCH’ là hình bình hành. Chứng minh rằng khi A thay đổi thì H’ luôn nằm trên đường tròn (C). Tìm tập hợp của H.
| Lời giải • Chứng minh H'\[\in \] (C) Tứ giác AB'HC' có: \[\widehat{AC'H}+\widehat{AB'H}={{90}^{0}}\] nên \[\widehat{C'AB'}+\widehat{B'HC'}={{180}^{0}}\] Mặt khác
\[\Rightarrow \widehat{C'AB'}+\widehat{H'}={{180}^{0}}\] Suy ra tứ giác ABHC nội tiếp đường tròn (C). Vậy H’ thuộc đường tròn (C). • Tập hợp của H. Gọi I là tâm của hình bình hành HBH’C. Ta có: \[\overrightarrow{H'I}=\overrightarrow{IH}\] nên Khi A chạy trên (C) thì H’ cũng chạy trên(C) nên tập hợp của H là đường tròn (C’) ảnh của (C) qua phép đối xứng tâm I nói trên. | Giải thích • Để chứng minh H' thuộc đường tròn (C), ta chứng minh tứ giác ABH’C nội tiếp đường tròn đó. • Một tứ giác nội tiếp đường tròn khi và chỉ khi tổng hai góc đối diện của nó bằng 180°.
|

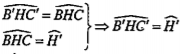
.png)