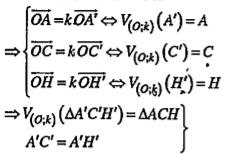.png)
| b) Lấy A(2;0)\[\in \] d. Gọi A" (x’;y’) =
d2//d \[\Rightarrow \]d1: 2x+y+m=0 A’ \[\in \] d2 \[\Leftrightarrow \]2.(-7)+6+m=0 \[\Leftrightarrow \] m=8 Vậy d2: 2x+y+8=0 | Cách làm tương tự câu a. Cần chú ý: \[\overrightarrow{IA''}=(x''-{{x}_{I}};y''-{{y}_{I}})\] \[\overrightarrow{IA}=({{x}_{A}}-{{x}_{I}};{{y}_{A}}-{{y}_{I}})\]
|
Bài 1.24. Trong mặt phẳng Oxy cho đường tròn (C): .png) . Hãy viết phương trình đường tròn (C’) là ảnh của (C) qua phép vị tự tâm I(1;2), tỉ số k=-2.
. Hãy viết phương trình đường tròn (C’) là ảnh của (C) qua phép vị tự tâm I(1;2), tỉ số k=-2.
| Lời giải
Gọi J’(x’;y’)=
Vậy (C’): | Giải thích Các bước thực hiện: • Bước 1: Xác định tâm J và bán kính R của (C). • Bước 2: Tìm tọa độ của J’ là ảnh của J qua phép vị tự đã cho. J’ chính là tâm của (C). • Bước 3: Tìm \[R'=k\left| R \right|\] là bán kính của (C). |
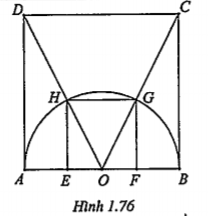
Bài 1.25. Cho nửa đường tròn đường kính AB. Hãy dựng hình vuông có hai đỉnh nằm trên nửa đường tròn, hai đỉnh còn lại nằm trên đường kính AB của nửa đường tròn đó.
| Lời giải • Phân tích: Giả sử đã đựng được hình vuông EFGH có hai đỉnh E, F nằm trên đường kính AB, hai đỉnh còn lại G, H thuộc nửa đường tròn đã cho. | Giải thích
|
| Thực hiện phép vị tự tâm O, tỉ số \[k=\frac{GH}{AB}\] thì hình vuông EFGH sẽ biến thành hình vuông ABCD. (H. 1.76) • Cách dựng: Dựng hình vuông ABCD nằm cùng phía với nửa đường tròn đường kính AB đối với đường thẳng AB. Gọi H, G lần lượt là giao điểm của DO, CO với nửa đường tròn. Dựng HE//AD (E\[\in \]AB), GF // BC (F\[\in \]AB). Khi đó tứ giác EFGH là hình vuông cần dựng. • Chứng minh: Theo cách dựng thì tứ giác EFGH có hai đỉnh nằm trên đường kính AB, hai đỉnh còn lại nằm trên nửa đường tròn. Áp dụng định lí Ta – let , ta có: \[\frac{\overrightarrow{OH}}{\overrightarrow{OD}}=\frac{\overrightarrow{OG}}{\overrightarrow{OC}}=\frac{\overrightarrow{OE}}{\overrightarrow{OA}}=\frac{\overrightarrow{OF}}{\overrightarrow{OB}}=k\]
\[\Rightarrow \] EFGH cũng là hình vuông. |
|
| • Biện luận: Ta luôn chỉ có một hình vuông duy nhất ABCD nằm cùng phía với nửa đường tròn đường kính AB đối với đường thẳng AB nên chỉ có một điểm H và một điểm G duy nhất. Vậy bài toán luôn có một nghiệm hình duy nhất. |
|
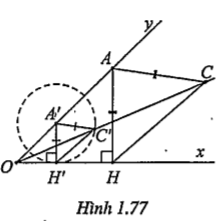
Bài 1.26.
| Lời giải • Phân tích: Giả sử đã dựng được điểm A trên cạnh Oy sao cho AH = AC (H là hình chiếu của A trên Ox). Lấy điểm A' bất kì trên Oy, gọi H’ là hình chiếu vuông góc của A’ trên Ox. Đường thẳng qua A’ song song với AC cắt đường thẳng OC tại C’. Khi đó, tam giác ACH là ảnh của tam giác A'C’H’ qua phép vị tự tâm O tỉ số \[k=\frac{AC}{A'C'}\] nên A'C’=A'H'. Từ đó suy ra cách dựng: • Cách dựng: Dựng điểm A' bất kì trên Oy, dựng H’ là hình chiếu vuông góc của A' trên Ox. Dựng đường tròn tâm A’ bán kính A’H’ cắt OC tại C’. Dựng đường thẳng qua C song song với A'C'. Đường thẳng này cắt Oy tại A. Khi đó A là điểm cần đựng. | Giải thích
|
| • Chứng minh: Vì A'C// AC nên: \[\frac{\overrightarrow{OA}}{\overrightarrow{OA'}}=\frac{\overrightarrow{OC}}{\overrightarrow{OC'}}=\frac{\overrightarrow{OH}}{\overrightarrow{OH'}}=k\]
\[\Rightarrow AC=AH\] • Biện luận: Vì đường tròn tâm A’ bán kính A'H' luôn cắt đường thẳng OC tại hai điểm phân biệt nên bài toán luôn có hai nghiệm hình. |
|

.png) = A" .
= A" ..png)
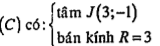
.png) \[\Leftrightarrow \overrightarrow{IJ'}=-2\overrightarrow{IJ}\]
\[\Leftrightarrow \overrightarrow{IJ'}=-2\overrightarrow{IJ}\] 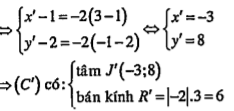
.png)