C. CÂU HỎI VÀ BÀI TẬP.
Bài 3.8. Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng \[\overrightarrow{G\text{D}}.\overrightarrow{GA}+\overrightarrow{G\text{D}}.\overrightarrow{GB}+\overrightarrow{G\text{D}}.\overrightarrow{GC}=0\].
| Lời giải Ta có: \[\overrightarrow{G\text{D}}.\overrightarrow{GA}+\overrightarrow{G\text{D}}.\overrightarrow{GB}+\overrightarrow{G\text{D}}.\overrightarrow{GC}\] \[=\overrightarrow{G\text{D}}\left( \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC} \right)\] = 0 | Giải thích Vì G là trọng tâm của tam giác ABC nên: \[\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\]=0 |
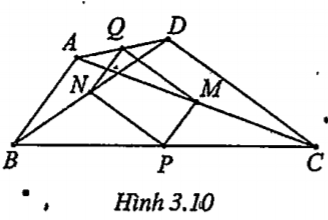
Bài 3.9. Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn AC, BD, BC, AD và có MN = PQ . Chứng minh rằng AB ⊥ CD.
| Lời giải
\[\Rightarrow \]MPNQ là hình chữ nhật. Do đó \[\overrightarrow{QN}.\overrightarrow{QM}=0\] Ta có: \[\overrightarrow{AB}.\overrightarrow{C\text{D}}=2\overrightarrow{QN}.\overrightarrow{QM}=2.0=0\] \[\Rightarrow \overrightarrow{AB}\bot \overrightarrow{C\text{D}}\]. Vậy AB ⊥ CD. | Giải thích • Cần chứng minh: \[\overrightarrow{AB}.\overrightarrow{C\text{D}}=0\] • Ta có MQ, NP lần lượt là đường trung bình của tam giác ACD và BCD. • Hình bình hành MPNQ có hai đường chéo MN, PQ bằng nhau nên nó là hình chữ nhật.
|
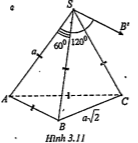
Bài 3.10. Cho hình chóp tam giác S.ABC có \[SA=SB=SC=AB=AC=a\] và \[BC=a\sqrt{2}\]. Tính góc giữa hai vectơ \[\overrightarrow{AB}\] và \[\overrightarrow{SC}\]
| Lời giải \[\Delta ABC\] vuông có AB=AC=a, \[BC=a\sqrt{2}\] \[\Rightarrow \Delta ABC\] vuông tại A\[\Rightarrow AB\bot AC\] Ta có: \[\overrightarrow{AB}.\overrightarrow{SC}=\overrightarrow{AB}.\left( \overrightarrow{SA}+\overrightarrow{AC} \right)\] \[=\overrightarrow{AB}.\overrightarrow{SA}+\overrightarrow{AB}.\overrightarrow{AC}\] \[=AB.SA.\cos \left( \overrightarrow{AB},\overrightarrow{SA} \right)\] \[={{a}^{2}}.\cos {{120}^{0}}=-\frac{{{a}^{2}}}{2}\] | Giải thích \[A{{B}^{2}}+A{{C}^{2}}={{a}^{2}}+{{a}^{2}}=2{{a}^{2}}\] \[B{{C}^{2}}={{\left( a\sqrt{2} \right)}^{2}}=2{{a}^{2}}\] \[\Rightarrow A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}}\] \[\Rightarrow \Delta ABC\] vuông tại A\[\Rightarrow \overrightarrow{AB}.\overrightarrow{AC}=0\] Để xác định góc giữa hai vectơ \[\overrightarrow{AB}\] và \[\overrightarrow{SC}\] , ta vẽ vectơ \[\overrightarrow{SB'}=\overrightarrow{AB}\] Khi đó: \[\left( \overrightarrow{SA},\overrightarrow{AB} \right)=\left( \overrightarrow{SA},\overrightarrow{SB'} \right)\] = |
| Khi đó: \[\cos \left( \overrightarrow{SC},\overrightarrow{AB} \right)=\frac{\overrightarrow{SC}.\overrightarrow{AB}}{\left| \overrightarrow{SC} \right|.\left| \overrightarrow{AB} \right|}=\frac{-\frac{{{a}^{2}}}{2}+0}{{{a}^{2}}}=-\frac{1}{2}\] Vậy \[\left( \overrightarrow{SC},\overrightarrow{AB} \right)={{120}^{0}}\] |
|
Bài 3.11. Cho hình chóp tam giác S.ABC có SA = SB = SC = AB = AC = a và \[BC=a\sqrt{2}\]. Tính góc giữa hai đường thẳng AB và SC.
| Lời giải
Ta có: \[\overrightarrow{SC}.\overrightarrow{AB}=\left( \overrightarrow{SA}+\overrightarrow{AC} \right).\overrightarrow{AB}\]\[=\overrightarrow{SA}.\overrightarrow{AB}+\overrightarrow{AC}.\overrightarrow{AB}\] \[\left| \overrightarrow{SA} \right|.\left| \overrightarrow{AB} \right|.\cos {{120}^{\circ }}=-\frac{{{a}^{2}}}{2}\] Khi đó: \[\cos \left( \overrightarrow{SC},\overrightarrow{AB} \right)=\frac{\overrightarrow{SC}.\overrightarrow{AB}}{\left| \overrightarrow{SC} \right|.\left| \overrightarrow{AB} \right|}\]\[=\frac{-\frac{{{a}^{2}}}{2}}{{{a}^{2}}}=-\frac{1}{2}\] Vậy \[\left( \overrightarrow{SC},\overrightarrow{AB} \right)={{60}^{0}}\] | Giải thích • Để xác định góc giữa hai đường thẳng, ta xác định vectơ chỉ phương của chúng. Ở đây, vectơ chỉ phương của hai đường thẳng AB, SA lần lượt là \[\cos \left( \overrightarrow{SC},\overrightarrow{AB} \right)=\frac{\overrightarrow{SC}.\overrightarrow{AB}}{\left| \overrightarrow{SC} \right|.\left| \overrightarrow{AB} \right|}\] • Độc giả cần chú ý đến sự khác nhau giữa công thức tính góc giữa hai vectơ (nhọn hoặc tù) và góc giữa hai đường thẳng (nhọn hoặc vuông) |
Bài 3.12. Chứng minh rằng một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
| Lời giải Giả sử ta có hai đường thẳng d và d’ song song với nhau và vectơ \[\overrightarrow{u}=\left( a,b \right)\] là một vectơ chỉ phương của d Đường thẳng d1 vuông góc với d nên có vectơ chỉ phương là n=\[\left( -b,a \right)\]
Vì d và d’ song song nên vectơ \[\overrightarrow{u}=\left( a,b \right)\] cũng là một vectơ chỉ phương của d’. Ta có: \[\overrightarrow{u}.\overrightarrow{n}=a.\left( -b \right)+b.a=0\] \[\overrightarrow{u}\bot \overrightarrow{n}\Rightarrow {{d}_{1}}\bot d'\] | Giải thích Chú ý. • Hai đường thẳng vuông góc với nhau thì các vectơ chỉ phương của chúng cũng vuông góc với nhau (tích vô hướng bằng 0). • Hai đường thẳng song song có cùng vectơ chỉ phương.
|
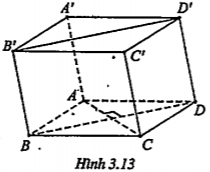
Bài 3.13. Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau ( hình hộp như vậy còn được gọi là hình hộp thoi). Chứng minh rằng AC ⊥ B’D’
| Lời giải Ta có ABCD là hình thoi nên AC ⊥ BD Mặt khác BDD’B’ là hình bình hành nên BD//B’D’ Vậy AC ⊥ B’D’ | Giải thích Áp dụng định lý 22
|
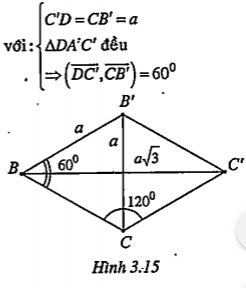
Bài 3.14. Cho hình hộp thoi ABCD.A'B'C'D' có tất cả các cạnh đều bằng a và \[\widehat{ABC}=\widehat{{B}'BA}=\widehat{{B}'BC}={{60}^{0}}\]. Chứng minh rằng tứ giác A'B'CD là hình vuông
| Lời giải Hình thoi BCC'B' có \[\widehat{{B}'BC}={{60}^{0}}\]nên đường chéo B’C= a (H.3.15). Tứ giác CDA'B' có: B'C = A'D=A'B' = CD = a nên là hình thoi. Ta chứng minh hình thoi này có \[CD\bot CB'\]
| Giải thích \[\overrightarrow{CB}.\overrightarrow{CB'}=CB.CB'.cos\left( \overrightarrow{CB},\overrightarrow{CB'} \right)\] Với CB=CB’=a \[\left( \overrightarrow{CB},\overrightarrow{CB'} \right)={{60}^{0}}\] \[\overrightarrow{BC'}.\overrightarrow{CB'}=BC'.CB'.cos\left( \overrightarrow{BC'},\overrightarrow{CB'} \right)\] Với \[BC'=a\sqrt{3},CB'=a\] \[\left( \overrightarrow{BC'},\overrightarrow{CB'} \right)={{90}^{0}}\] \[\Rightarrow \overrightarrow{BC'}.\overrightarrow{CB'}=0\] |
| Ta có: \[\overrightarrow{C{B}'}.\overrightarrow{CD}=\left( \overrightarrow{CB}+\overrightarrow{B{B}'} \right).\overrightarrow{BA}\] \[=\overrightarrow{CB}.\overrightarrow{BA}+\overrightarrow{B{B}'}.\overrightarrow{BA}\] \[=-\frac{{{a}^{2}}}{2}+\frac{{{a}^{2}}}{2}=0\] \[\Rightarrow CD\bot CB'\] Vậy tứ giác A'B'CD là hình vuông vì nó là hình thoi có một góc vuông.
| Vì \[\overrightarrow{C'D}=-\overrightarrow{DC'}\] nên \[\overrightarrow{C'D}.\overrightarrow{CB'}=-\overrightarrow{DC'}.\overrightarrow{CB'}\] \[=-DC'.CB'.\cos \left( \overrightarrow{DC'},\overrightarrow{CB'} \right)\]
|
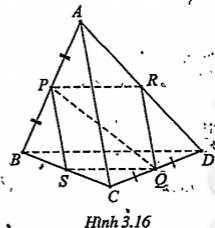
Bài 3.15. Cho tứ diện ABCD trong đó \[AB\bot AC,AB\bot B\text{D}\]. Gọi P, Q lần lượt là trung điểm của AB và CD. Chứng minh rằng AB và PQ vuông góc với nhau.
| Lời giải Ta có: \[AB\bot AC\Rightarrow \overrightarrow{AB}.\overrightarrow{AC}=0(1)\] \[AB\bot B\text{D}\Rightarrow \overrightarrow{AB}.\overrightarrow{BD}=0(2)\] (1)+(2) \[\Rightarrow \overrightarrow{AB}.\overrightarrow{AC}+\overrightarrow{AB}.\overrightarrow{BD}=0\] \[=\overrightarrow{AB}.(\overrightarrow{AC}+\overrightarrow{BD})\] (3) Gọi R và S lần lượt là trung điểm của AD và BC, ta có: \[(3)\Rightarrow 2\overrightarrow{AB}(\overrightarrow{RQ}+\overrightarrow{SQ})=0\] \[\Rightarrow \overrightarrow{AB}(\overrightarrow{RQ}+\overrightarrow{PR})=0\Rightarrow \overrightarrow{AB}.\overrightarrow{PQ}=0\] Vậy \[AB\bot PQ\] | Giải thích Để ý rằng tứ giác PRQS là hình bình hành. Ta có: \[\overrightarrow{AC}=2\overrightarrow{RQ}\] , \[\overrightarrow{BD}=2\overrightarrow{SQ}\] , \[\overrightarrow{SQ}=\overrightarrow{PR}\]
|

.png)
.png)
.png)
.png) rồi áp dụng công thức:
rồi áp dụng công thức: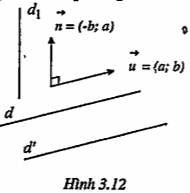
.png)