B. DẠNG TOÁN CƠ BẢN
Vấn đề 1. Chứng minh các đẳng thức về vectơ
1. Phương pháp
Để xác định các yếu tố của một vectơ, ta dựa vào định nghĩa các yếu tố của vectơ, các tính chất hình học của hình đã cho.
2. Ví dụ
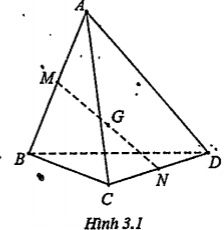
Ví dụ. Chứng minh rằng G là trọng tâm của tứ diện ABCD khi và chỉ khi nó thỏa mãn một trong hai điều kiện sau:
\[a)\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\]
\[b)\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=4\overrightarrow{OG}\] (Với O là điểm tùy ý)
| Lời giải Gọi M và N lần lượt là trung điểm của AB và CD, ta có: \[\overrightarrow{GA}+\overrightarrow{GB}=2\overrightarrow{GM}~\] \[\overrightarrow{GC}+\overrightarrow{GD}=2\overrightarrow{GN}\] Như vậy: \[a)\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\] \[\Leftrightarrow 2(\overrightarrow{GM}+\overrightarrow{GN})=\overrightarrow{0}\] \[\Leftrightarrow \] G là trung điểm của MN \[\Leftrightarrow \] G là trọng tâm của tứ diện ABCD. | Giải thích Áp dụng quy tắc trung điểm.
|
| \[b)\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}\] \[\Leftrightarrow \overrightarrow{OA}-\overrightarrow{OG}+\overrightarrow{OB}-\overrightarrow{OG}+\overrightarrow{OC}-\overrightarrow{OG}+\overrightarrow{OD}-\overrightarrow{OG}=\overrightarrow{0}\] \[\Leftrightarrow \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}-4\overrightarrow{OG}=\overrightarrow{0}\] \[\Leftrightarrow \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=4\overrightarrow{OG}\] |
|