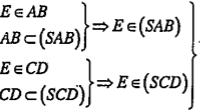B. DẠNG TOÁN CƠ BẢN
Vấn đề 1. Xác định giao tuyến của hai mặt phẳng
1. Phương pháp
Để tìm giao tuyến của hai mặt phẳng ta tìm hai điểm chung của chúng, đường thẳng đi qua hai điểm chung này là giao tuyến cần tìm.
2. Ví dụ
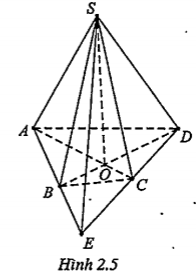
Ví dụ. Cho tứ giác ABCD (không có cặp cạnh đối nào song song) nằm trong mặt phẳng \[(\alpha )\]. S là điểm không nằm trên \[(\alpha )\]. Tìm giao tuyến của các cặp mặt phẳng: (SAC) và (SBD), (SAB) và (SCD).
| Lời giải Giao tuyến của (SAC) và (SBD): Gọi O là giao điểm của hai đường chéo AC và BD. Ta có: | Giải thích S là điểm chung thứ nhất. Điểm chung thứ hai là giao điểm O của AC và BD |
|
(1) suy ra: S là điểm chung thứ nhất.
\[\Rightarrow O\in (SAC)\cap (SBD)\] (2) (2) suy ra O là điểm chung thứ hai. Vậy: \[SO=(SAC)\cap (SBD)\] |
|
| Giao tuyến của (SAB) và (SCD) Gọi E là giao điểm của AB và CD. Ta có:
(3) suy ra S là điểm chung thứ nhất.
\[\Rightarrow E=(SAB)\cap (SCD)\] (4) (4) suy ra: E là điểm chung thứ hai. Vậy \[SE=(SAB)\cap (SCD)\] | S là điểm chung thứ nhất. Điểm chung thứ hai là giao điểm của AB và CD.
|

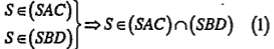
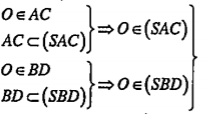
.png)