Vấn đề 2. Dựng mặt phẳng chứa đường thẳng cho trước và vuông góc với mặt phẳng cho trước
1. Phương pháp
Cho đường thẳng a không vuông góc với mặt phẳng (P). Để đựng mặt phẳng (Q) chứa a và vuông góc với (P) ta làm như sau:
• Lấy điểm M thuộc a.
• Dựng qua M đường thẳng b vuông góc với (P).
Khi đó mặt phẳng (a, b) chính là mặt phẳng (Q) cần dựng.
2. Ví dụ
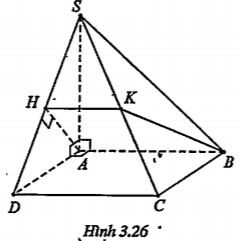
Ví dụ. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với mặt phẳng đáy (ABCD). Gọi (\[\alpha \]) là mặt phẳng chứa AB và vuông góc với mặt phẳng (SCD). Hãy xác định mặt phẳng (\[\alpha \]). Mặt phẳng (\[\alpha \]) cắt hình chóp đã cho theo thiết diện là hình gì?
| Lời giải • Xác định (\[\alpha \]) Trong mặt phẳng (SAD), gọi H là hình chiếu vuông góc của A trên SD. Ta có: AB\[\bot \] (SAD) AB//CD \[\Rightarrow \]CD\[\bot \] (SAD) (SAD) \[\supset \]AH \[\Rightarrow \]AH\[\bot \]CD Mặt khác AH\[\bot \]SD \[\Rightarrow \]AH\[\bot \] (SCD) \[\Rightarrow \] (AH,AB)\[\bot \] (SCD) Ta thấy (AH, AB) \[\supset \]AH và (AH,AB)\[\bot \] (SCD) nên (\[\alpha \])\[\equiv \] (AH,AB). | Giải thích AB\[\bot \]SA AB\[\bot \]AD ⇒ AB\[\bot \] (SAD). (AH, AB) \[\supset \]AH AH\[\bot \] (SCD) \[\Rightarrow \] (AH,AB)\[\bot \] (SAD)
|
| • Thiết diện của (\[\alpha \]) với hình chóp Ta có: H\[\in \] (\[\alpha \])\[\cap \] (SCD) (\[\alpha \])\[\supset \]AB,(SCD) \[\supset \]CD AB// CD \[\Rightarrow \] (\[\alpha \])\[\cap \] (SCD)=HK, HK//AB (K\[\in \]SC) Vậy thiết diện cần tìm là tứ giác ABKH có HK//AB, \[AB\bot AH\] nên nó là hình thang vuông. | Ta tìm giao điểm K của SC và mặt phẳng (\[\alpha \]) |