Chương I.
PHÉP DỜI HÌNH VÀ PHÉP ĐỒNG DẠNG TRONG MẶT PHẲNG
§1. PHÉP BIẾN HÌNH
§2. PHÉP ĐỒNG DẠNG
A. CÁC KIẾN THỨC CẦN NHỚ
I. PHÉP BIẾN HÌNH
Định nghĩa.
Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M' của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng.
Kí hiệu phép biến hình là F và viết F(M)=M' hay M' =F(M).
Nếu ℋ đó là một hình nào đó trong mặt phẳng thì ta kí hiệu H'=F(H) là tập hợp các điểm M’ = F(M), với mọi điểm M thuộc ℋ. Khi đó ta nói F biến hình ℋ thành hình ℋ’, hay hình ℋ ‘ là ảnh của hình ℋ qua phép biến hình F.
Để chứng minh hình ℋ’ là ảnh của hình ℋ qua phép biến hình F ta có thể chứng minh:
Với điểm M tùy ý, M ∈ ℋ \[\Leftrightarrow \]M’=F(M) ∈( ℋ’).
Phép biến hình biến mỗi điểm M của mặt phẳng thành chính nó được gọi là phép đồng nhất.
II. PHÉP TỊNH TIẾN
Định nghĩa
Trong mặt phẳng cho vectơ \[\overrightarrow{v}\]. Phép biến hình biến mỗi điểm M thành điểm đến M' sao cho \[\overrightarrow{MM'}=\overrightarrow{v}\] được gọi là phép tịnh tiến theo vectơ \[\overrightarrow{v}\]. Kí hiệu: \[{{T}_{\overrightarrow{v}}}\]
Như vậy: \[{{T}_{\overrightarrow{v}}}=M'\Leftrightarrow \overrightarrow{MM'}=\overrightarrow{v}\]
Chú ý. Phép tịnh tiến theo vectơ – không là phép đồng nhất.
III. BIỂU THỨC TỌA ĐỘ CỦA PHÉP TÍNH TIẾN
Trong mặt phẳng Oxy cho điểm M(x;y), \[\overrightarrow{v}=(a,b).\] Khi đó:
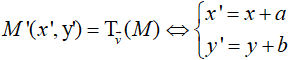
IV. TÍNH CHẤT CỦA PHÉP TỊNH TIẾN
Phép tịnh tiến:
1. Bảo toàn khoảng cách giữa hai điểm bất kì:
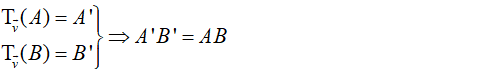
2. Biến một đường thẳng thành một đường thẳng song song hoặc trùng với nó:
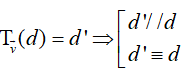
3. Biến đoạn thẳng thành đoạn thẳng bằng đoạn thẳng đã cho:
\[{{T}_{\overrightarrow{v}}}(AB)=A'B'\Rightarrow A'B'=AB\]
4. Biến tam giác thành tam giác bằng tam giác đã cho:
\[{{T}_{\overrightarrow{v}}}(\Delta ABC)=\Delta A'B'C'\Rightarrow \Delta ABC=\Delta A'B'C'\]
5. Biến đường tròn thành đường tròn có cùng bán kính:
\[{{T}_{\overrightarrow{v}}}(O;R)=(O';R)\]
