C. CÂU HỎI VÀ BÀI TẬP
Bài1.27. Trong mặt phẳng Oxy cho đường thẳng d có phương trình \[x=2\sqrt{2}\]. Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số \[k=\frac{1}{2}\]và phép quay tâm O góc 45°.
| Lời giải • Ta có: \[A(2\sqrt{2};0)\in d\] Gọi A’(x’,y’)= \[{{V}_{(o;\frac{1}{2})}}\](A) \[\overrightarrow{OA'}=\frac{1}{2}\overrightarrow{OA}\]
Gọi d1=\[{{V}_{(o;\frac{1}{2})}}\](d) thì
• Gọi A’’(x’’;y’’)= | Giải thích Các bước thực hiện: • Bước 1: Xác định ảnh A’ của A qua phép vị tự \[{{V}_{(o;\frac{1}{2})}}\] • Bước 2: Xác định ảnh A” của A' qua phép quay |
| là giao điểm của tia phân giác góc vuông thứ nhất \[\Delta \] và đường tròn (C) tâm O bán kính\[R=\sqrt{2}\]. Suy ra tọa độ giao điểm của A” là nghiệm của hệ:
Vì d’ tạo với d một góc 45° nên d’ tạo với trục Ox một góc 135° Hệ số góc của d’ là k=tan135° =-1 nên ta có thể chọn \[\overrightarrow{u}\]=(-1;1) làm một vectơ chỉ phương của d’. Suy ra một vectơ pháp tuyến của d’ là \[\overrightarrow{n}=(1;1)\] Tóm lại, đường thẳng d đi qua A” và có vectơ pháp tuyến \[\overrightarrow{n}=(1;1)\] nên có phương trình x+y-2=0. |
Chú ý. 1. Để tìm ảnh A” của A' qua phép quay tâm O góc 45°, ta cần chú ý rằng vì A' thuộc trục hoành nên A” phải nằm trên tia phân giác thứ nhất của góc phần tư thứ nhất của hệ trục tọa độ. Mặt khác, theo định nghĩa của phép quay thì OA'=OA” nên A” phải nằm trên đường tròn tâm O bán kính \[R=\sqrt{2}\] Nhận xét này giúp ta giải bài toán tổng quát: Tìm ảnh của một điểm bất kì qua phép quay có tâm và góc quay bất kì nào đó. 2. Khi biết góc giữa đường thẳng và trục Ox thì ta hoàn toàn xác định được một vectơ chỉ phương của đường thẳng đó. |
Bài 1.28. Trong mặt phẳng Oxy cho đường tròn .png) . Hãy viết phương trình đường tròn (C') là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Ox và phép vị tự tâm O tỉ số k= 2.
. Hãy viết phương trình đường tròn (C') là ảnh của (C) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng qua trục Ox và phép vị tự tâm O tỉ số k= 2.
| Lời giải • Đường tròn (C) có tâm I(1;2), bán kính R=2. Gọi (C’)= Đường tròn (C’) có tâm I’(1;-2), bán kính R=2. • Gọi I’’=
Gọi
| Giải thích
|
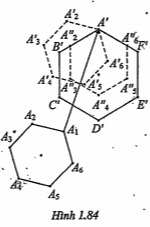
Bài 1.29. Chứng minh rằng hai đa giác đều có cùng số cạnh luôn đồng dạng với nhau.
| Lời giải Giả sử có hai n – giác đều A1A2...An, và A’1A’2...A’n • Phép tịnh tiến \[{{T}_{\overrightarrow{{{A}_{1}}A'}}}\] biến đa giác đều A1A2...An thành đa giác đều A’1A’2...A’n • Phép quay • Phép vị tự Vậy phép đồng dạng có được bằng cách thực hiện liên tiếp các phép biến hình \[{{T}_{\overrightarrow{{{A}_{1}}A'}}}\], |
|
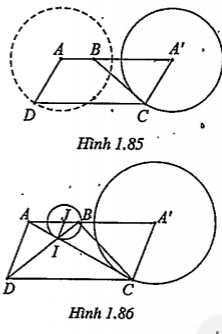
Bài 1.30. Cho hình thang ABCD có AB song song với CD, AD = a, DC = b còn hai đỉnh A, B cố định. Gọi I là giao điểm của hai đường chéo.
a) Tìm tập hợp các điểm C khi D thay đổi.
b) Tìm tập hợp các điểm I khi C và D thay đổi như trong câu a).
| Lời giải a) Tập hợp của C: Vì AD = a không đổi nên D chạy trên đường tròn (C) tâm A bán kính bằng a. Dựng điểm A' sao cho tứ giác AA'CD là hình bình hành. Khi đó A' (cố định) là ảnh của A qua phép tịnh tiến vectơ \[\overrightarrow{AA'}\] Vậy khi D chạy trên (C) thì C chạy trên đường tròn (C’) là ảnh của (C) qua phép tịnh tiến nói trên. Kết luận: Tập hợp của C là đường tròn tâm A’, bán kính bằng a (H. 1.85) b) Tập hợp của I: Ta có: \[\Delta AIB\sim \Delta CID\Leftrightarrow \frac{AI}{CI}=\frac{AB}{CD}\] (1) \[\Rightarrow \frac{AI}{AC}=\frac{AB}{AB+b}\] (2) \[\Rightarrow \overrightarrow{AI}=\frac{AB}{AB+b}\overrightarrow{AC}\] Đẳng thức cuối cùng chứng tỏ I là ảnh của C qua phép vị tự tâm A tỉ số \[k=\frac{AB}{AB+b}\]. Vậy khi C chạy trên (C’) thì I chạy trên đường tròn (C’’) là ảnh của (C’) qua phép vị tự nói trên. Kết luận: Tập hợp các điểm I là đường tròn (C’’) tâm \[J={{V}_{\left( A;k=\frac{AB}{AB+b} \right)}}(A')\] (H.1.86) | Giải thích • Vì AB // CD nên \[\Delta AIB\sim \Delta CID\] từ đó suy ra tỉ số đồng dạng (1) • (2) có được nhờ áp dụng tính chất của tỉ lệ thức: \[\frac{a}{b}=\frac{c}{d}\Rightarrow \frac{a}{a+b}=\frac{c}{c+d}\]
|

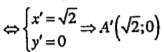
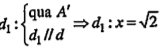
.png) thì A’’
thì A’’.png)
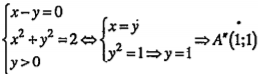
.png)
.png) thì phương trình của (C’):
thì phương trình của (C’): .png)
.png) thì
thì .png)
.png) thì đường tròn (C’’) có tâm I’’(-2;4), bán kính \[R''=\left| -2 \right|.R=4\] nên có phương trình \[(C''):{{\left( x+2 \right)}^{2}}+{{(y-4)}^{2}}=16\]
thì đường tròn (C’’) có tâm I’’(-2;4), bán kính \[R''=\left| -2 \right|.R=4\] nên có phương trình \[(C''):{{\left( x+2 \right)}^{2}}+{{(y-4)}^{2}}=16\] 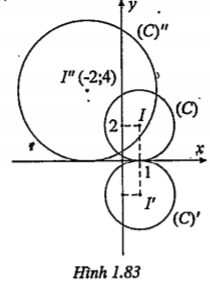
.png) với
với .png) biến đa giác đều A’1A’2...A’n thành đa giác đều A’1A’’2...A’’n
biến đa giác đều A’1A’2...A’n thành đa giác đều A’1A’’2...A’’n .png) với \[k=\frac{A'B'}{A{{'}_{1}}{{A}_{2}}'}\] biến đa giác đều A’1A’’2...A’’n thành đa giác đều A’1A’2...A’n
với \[k=\frac{A'B'}{A{{'}_{1}}{{A}_{2}}'}\] biến đa giác đều A’1A’’2...A’’n thành đa giác đều A’1A’2...A’n .png) ,
, .png) biến đa giác đều
biến đa giác đều .png) thành đa giác đều
thành đa giác đều .png) nên chúng đồng dạng với nhau.
nên chúng đồng dạng với nhau.