§4. PHÉP ĐỐI XỨNG TÂM

A. CÁC KIẾN THỨC CẦN NHỚ

1. ĐỊNH NGHĨA

1. Cho điểm I. Phép biến hình biến điểm I thành chính nó, biến mỗi điểm M khác I thành M’ sao cho I là trung điểm của đoạn thẳng MM’ được gọi là phép đối xứng tâm I.

Phép đối xứng tâm I thường được kí hiệu là

Từ định nghĩa, suy ra:

=M’\[\Leftrightarrow \overrightarrow{IM'}=\overrightarrow{MI}\]

Như vậy:

Nếu \[M\equiv I\] thì \[M'\equiv I\].

Nếu \[M\ne I\] thì M’= \[\Leftrightarrow \]I là trung điểm của MM’.

2. Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành chính nó. Khi đó H được gọi là hình có tâm đối xứng.

II. BIỂU THỨC TỌA ĐỘ

Trong mặt phẳng tọa độ Oxy cho điểm , gọi M(x;y) và M'(x’;y’) là ảnh của M qua phép đối xứng tâm I. Khi đó

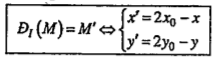
III. CÁC TÍNH CHẤT

Phép đối xứng tâm:

• Bảo toàn khoảng cách giữa hai điểm bất kì (H.1.31):

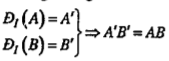
• Biến một đường thẳng thành một đường thẳng song song hoặc trùng với đường thẳng đã cho (H.1.32):

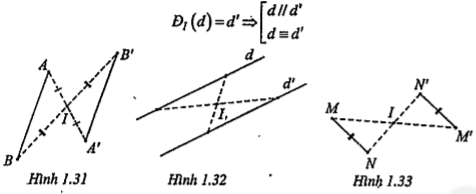
• Biến một đoạn thẳng thành một đoạn thẳng bằng đoạn thẳng đã cho (H.1.33):

= M'N'\[\Rightarrow \]M'N' = MN

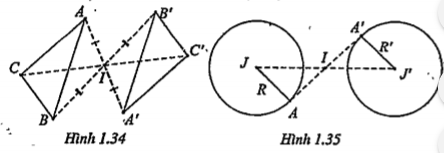
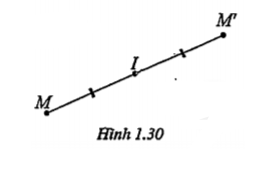
• Biến một tam giác thành một tam giác bằng tam giác đã cho (H 1.34):

=\[\Delta \] A'B'C'\[\Rightarrow \]\[\Delta \]A'B'C' =\[\Delta \]ABC

• Biến một đường tròn thành một đường tròn có cùng bán kính (H.1.35).

=(J’,R)