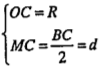Vấn đề 4. Dùng phép vị tự để tìm tập hợp điểm
1. Phương pháp
Để tìm tập hợp của điểm M’, ta thực hiện các bước sau:
• Bước 1: Xác định phép vị tự .png) =M’.
=M’.
• Bước 2: Tìm tập hợp H của M từ đó suy ra tập hợp của M' là hình H' ảnh của H qua phép vị tự trên.
2. Ví dụ
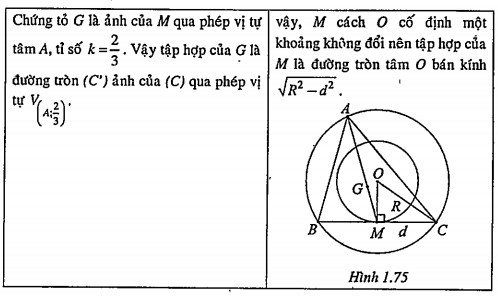
Ví dụ 1. Cho tam giác ABC nội tiếp đường tròn O bán kính R. M là trung điểm của BC, G là trọng tâm. Giả sử B, C di động, A cố định, hãy tìm tập hợp các điểm G.
| Lời giải Gọi M là trung điểm của BC thì \[OM\bot BC\] \[\Delta OMC\] có: \[\Rightarrow OM=\sqrt{O{{C}^{2}}-M{{C}^{2}}}=\sqrt{{{R}^{2}}-{{d}^{2}}}\] Suy ra: Tập hợp của M là đường tròn (C) tâm O bán kính \[\sqrt{{{R}^{2}}-{{d}^{2}}}\] Mặt khác: \[\frac{\overrightarrow{AG}}{\overrightarrow{AM}}=\frac{2}{3}\Leftrightarrow \overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM}\] | Giải thích Hướng dẫn. • Bài toán yêu cầu tìm tập hợp trọng tâm tam giác nên ta nghĩ ngay đến tính chất trọng tâm: \[\frac{\overrightarrow{AG}}{\overrightarrow{AM}}=\frac{2}{3}\Leftrightarrow \overrightarrow{AG}=\frac{2}{3}\overrightarrow{AM}\] (với M là trung điểm của BC). Cho nên, để tìm tập hợp của G, ta đi tìm tập hợp của M. • Vì R và d không đổi nên \[OM=\sqrt{{{R}^{2}}-{{d}^{2}}}\] không đổi. |