Vấn đề 2. Một số bài toán về mối liên quan giữa một số phép dời hình quen biết
1. Phương pháp
Dùng định nghĩa của các phép dời hình liên quan.
2. Ví dụ
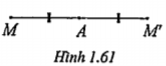
Ví dụ 1. Chứng minh rằng khi thực hiện liên tiếp hai phép đối xứng tâm A và đối xứng tâm B ta được phép tịnh tiến theo vectơ \[\overrightarrow{v}=2\overrightarrow{AB}\].
| Lời giải • \[\Leftrightarrow \overrightarrow{MM'}=2\overrightarrow{AM'}\] • \[\Leftrightarrow \overrightarrow{M'M''}=2\overrightarrow{M'B}\] Ta có: \[\overrightarrow{M'M''}=\overrightarrow{MM'}+\overrightarrow{M'M''}\] \[=2(\overrightarrow{AM'}+\overrightarrow{M'B})=2\overrightarrow{AB}\] Đẳng thức cuối cùng chứng tỏ M" là ảnh của M qua phép tịnh tiến theo vectơ \[\overrightarrow{v}=2\overrightarrow{AB}\]. Vậy khi thực hiện liên tiếp hai phép đối xứng tâm A và đối xứng tâm B ta được phép tịnh tiến theo vectơ \[\overrightarrow{v}=2\overrightarrow{AB}\]. | Giải thích Các bước thực hiện: • Bước 1: Gọi M là điểm bất kì. Tìm ảnh M' của M qua phép đối xứng tâm A. • Bước 2: Tìm ảnh M’’ của M' qua phép đối xứng tâm B. • Bước 3: Lí luận để có \[\overrightarrow{M'M''}=2\overrightarrow{AB}\] Chú ý. • Phép đối xứng tâm A biến M thành M’ thì A là trung điểm của MM’, tức là: \[\overrightarrow{MA}=\overrightarrow{AM'}\Leftrightarrow \overrightarrow{MM'}=2\overrightarrow{AM'}\]
• Nhắc lại: \[{{T}_{\overrightarrow{v}}}(M)=M'\Leftrightarrow \overrightarrow{v}=\overrightarrow{MM'}\] Với ba điểm A,B,C tùy ý, ta có quy tắc ba điểm như sau: \[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\]
|

.png)
.png) =M’’\[\Leftrightarrow \overrightarrow{M'B}=\overrightarrow{BM''}\]
=M’’\[\Leftrightarrow \overrightarrow{M'B}=\overrightarrow{BM''}\]