Vấn đề 2. Xác định phép vị tự biến điểm M cho trước thành điểm M' cho trước
1. Phương pháp
Ta có hai trường hợp sau:
Trường hợp 1. Cho trước tâm vị tự O, tìm tỉ số vị tự \[k=\frac{\overrightarrow{OM'}}{\overrightarrow{OM}}\]
Trường hợp 2. Cho trước tỉ số vị tự k, tìm điểm O chia đoạn MM' theo tỉ số k.
2. Ví dụ
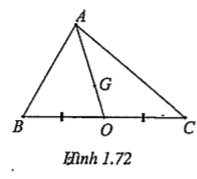
Ví dụ 1. Cho tam giác ABC có trọng tâm G. Hãy xác định tâm của phép vị tự có tỉ số \[k=\frac{1}{3}\] biến A thành G.
| Lời giải Ta có: G là trọng tâm \[\Delta \]ABC \[\Leftrightarrow \overrightarrow{OG}=\frac{1}{3}\overrightarrow{OA}\] (*) (với O là trung điểm của BC). Đẳng thức (*) chứng tỏ:
Vậy tâm của phép vị tự cần tìm là trung điểm O của BC. | Giải thích
|
Ví dụ 2. Gọi G, H, O lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác ABC.
a) Chứng minh rằng ba điểm G, H, O nằm trên một đường thẳng.
b) Tìm tỉ số của phép vị tự biến G thành H.
Chú ý. Đường thẳng đi qua trọng tâm, trực tâm và tâm đường tròn ngoại tiếp tam giác nói ở trên được gọi là đường thẳng Ơle.
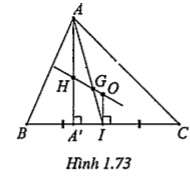
| Lời giải a) Ta có: Gọi I là trung điểm của BC\[\Rightarrow OI\bot BC\], \[AH\bot BC\] tại H.
\[\Rightarrow \frac{OI}{AH}=\frac{1}{2}\] \[\Rightarrow \overrightarrow{AH}=2\overrightarrow{OI}\] (1) Mặt khác: \[\overrightarrow{OB}+\overrightarrow{OC}=2\overrightarrow{OI}\] (2) Lại có: \[\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}\] (3) (2) và (3) \[\Rightarrow \overrightarrow{OA}+2\overrightarrow{OI}=3\overrightarrow{OG}\] (4) (1) và (4) \[\Rightarrow \overrightarrow{OA}+\overrightarrow{AH}=3\overrightarrow{OG}\] \[\Leftrightarrow \overrightarrow{OH}=3\overrightarrow{OG}\] (5) (5) chứng tỏ O, G, H thẳng hàng. | Giải thích Nhắc lại: • Ba điểm A,B,C phân biệt thẳng hàng \[\Leftrightarrow \overrightarrow{AB}=k\overrightarrow{AC}(k\ne 0)\] • G là trọng tâm tam giác ABC, ta có các kết quả sau: GA=2GI \[\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=3\overrightarrow{OG}\] (với O là điểm tùy ý)
|
| b) Đẳng thức (5) chứng tỏ H là ảnh của G qua phép vị tự |

.png)
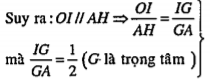
.png) tâm O, tỉ số k =3.
tâm O, tỉ số k =3.