C. CÂU HỎI VÀ BÀI TẬP
Bài 3.1. Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi O và O’ lần lượt là tâm của hai hình vuông ABCD và A'B'C'D'.
a) Hãy biểu diễn các vectơ \[\overrightarrow{AO},\overrightarrow{A{O}'}\] theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.
b) Chứng minh rằng \[\overrightarrow{A\text{D}}+\overrightarrow{{D}'{C}'}+\overrightarrow{{D}'{A}'}=\overrightarrow{AB}\]
| Lời giải a) Biểu diễn. \[\overrightarrow{AO}=\frac{1}{2}\overrightarrow{AC}=\frac{1}{2}\overrightarrow{{A}'{C}'}=\frac{1}{2}\left( \overrightarrow{AB}+\overrightarrow{A\text{D}} \right)\] \[=\frac{1}{2}\left( \overrightarrow{A'B'}+\overrightarrow{A'\text{D }\!\!'\!\!\text{ }} \right)\] \[=\frac{1}{2}\left( \overrightarrow{DC}+\overrightarrow{BC} \right)=\frac{1}{2}\left( \overrightarrow{D'C'}+\overrightarrow{B'C'} \right)\] \[\overrightarrow{AO'}=\frac{1}{2}\left( \overrightarrow{AA'}+\overrightarrow{AC'} \right)=\frac{1}{2}\left( \overrightarrow{AB'}+\overrightarrow{AD'} \right)\] \[=\frac{1}{2}\overrightarrow{AC}+\overrightarrow{A{A}'}\] \[=\overrightarrow{A{B}'}+\frac{1}{2}\overrightarrow{{B}'{D}'}\] \[=\overrightarrow{AB}+\overrightarrow{B{B}'}+\frac{1}{2}\overrightarrow{{B}'{D}'} =...\]
| Giải thích Ta có thể dùng quy tắc hình bình hành, quy tắc ba điểm,... để phân tích vectơ đã cho thành tổng, hiệu các vectơ theo yêu cầu đề bài.
|
| b) Chứng minh
| Để chứng minh một đẳng thức vectơ, ta thường phân tích vế phức tạp về vế đơn giản hơn. Ở đây ta phân tích vế trái thành vế phải. |
Bài 3.2. Trong không gian cho điểm O và bốn điểm A, B, C, D phân biệt và không thẳng hàng. Chứng minh rằng điều kiện cần và đủ để bốn điểm A, B, C, D tạo thành một hình bình hành là \[\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{O\text{D}}\]
Lời giải
Ta có: \[\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{O\text{D}}\]
\[\Leftrightarrow \overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{OD}-\overrightarrow{OC}\]
\[\Leftrightarrow \overrightarrow{BA}=\overrightarrow{CD}\] \[\Leftrightarrow \]ABCD là hình bình hành (vì bốn điểm ABCD không thẳng hàng)
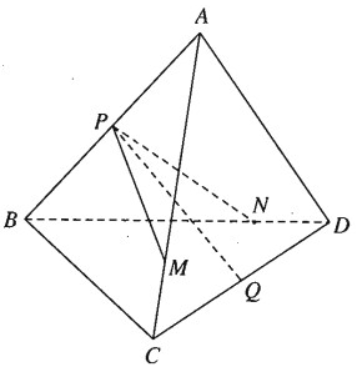
Bài 3.3. Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD ta lần lượt lấy các điểm M, N sao cho \[\frac{AM}{AC}=\frac{BN}{B\text{D}}=k\left( k>0 \right)\].
Chứng minh rằng ba vectơ \[\overrightarrow{PQ},\overrightarrow{PM},\overrightarrow{PN}\] đồng phẳng.
Lời giải
Ta có:
\[\overrightarrow{PQ}=\frac{1}{2}\left( \overrightarrow{PC}+\overrightarrow{P\text{D}} \right)\]
\[=\frac{1}{2}\left[ \left( \overrightarrow{AC}-\overrightarrow{AP} \right)+\left( \overrightarrow{B\text{D}}-\overrightarrow{BP} \right) \right]\]
\[=\frac{1}{2}\left[ \left( \overrightarrow{AC}+\overrightarrow{B\text{D}} \right)-\underset{{\vec{0}}}{\mathop{\underset{}{\mathop{\left( \overrightarrow{AP}+\overrightarrow{BP} \right)}}\,}}\, \right]\]
\[=\frac{1}{2}.\frac{1}{k}\left( \overrightarrow{AM}+\overrightarrow{BN} \right)\]
Vì \[\overrightarrow{AC}=\frac{1}{k}.\overrightarrow{AM}\] và \[\overrightarrow{B\text{D}}=\frac{1}{k}.\overrightarrow{BN}\]
Đồng thời \[\overrightarrow{AM}=\overrightarrow{AP}+\overrightarrow{PM}\] và \[\overrightarrow{BN}=\overrightarrow{BP}+\overrightarrow{PN}\] nên \[\overrightarrow{PQ}=\frac{1}{2k}\left( \overrightarrow{PM}+\overrightarrow{PN} \right)\]
Vì \[\overrightarrow{AP}+\overrightarrow{BP}=\vec{0}\]
Vậy \[\overrightarrow{PQ}=\frac{1}{2k}\overrightarrow{PM}+\frac{1}{2k}\overrightarrow{PN}\]
Do đó ba vectơ \[\overrightarrow{PQ},\overrightarrow{PM},\overrightarrow{PN}\] đồng phẳng.
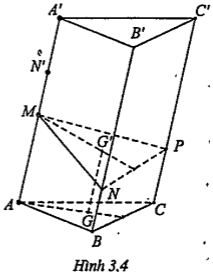
Bài 3.4. Cho hình lăng trụ tam giác ABC.A’B’C’ có độ dài cạnh bên bằng a. Trên các cạnh bên AA’,BB’,CC’ ta lấy tương ứng các điểm M, N, P sao cho \[AM+BN+CP=a\]
Chứng minh rằng mặt phẳng (MNP) luôn luôn đi qua một điểm cố định.
| Lời giải Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và tam giác MNP . Ta có: \[\overrightarrow{G{G}'}=\overrightarrow{GB}+\overrightarrow{BN}+\overrightarrow{N{G}'}\] (2) \[\overrightarrow{G{G}'}=\overrightarrow{GC}+\overrightarrow{CP}+\overrightarrow{P{G}'}\] (3) (1)+(2)+(3) ta được: \[+\left( \overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP} \right)+\left( \overrightarrow{M{G}'}+\overrightarrow{N{G}'}+\overrightarrow{P{G}'} \right)\] \[\Rightarrow 3\overrightarrow{G{G}'}=\overrightarrow{A{A}'}\Rightarrow \overrightarrow{G{G}'}=\frac{1}{3}\overrightarrow{A{A}'}\] Vì AA' không đổi nên \[\overrightarrow{AA'}\] cố định và G cố định nên \[\overrightarrow{GG'}\] cố định do đó G’ cố định. Vậy mặt phẳng (MNP) luôn đi qua điểm cố định G’.
| Giải thích Trên cạnh AA' ta lấy các điểm M, N’ sau đó lấy N trên BB’ sao cho BN=MN’, lấy P trên CC’ sao cho CP=N’A’ khi đó: • AM + BN +CP= a, và
Ta cũng chú ý rằng G và G’ tương ứng là trọng tâm các tam giác ABC và MNP nên:. \[\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0},\]và \[\overrightarrow{MG'}+\overrightarrow{NG'}+\overrightarrow{PG'}=\overrightarrow{0}\]
|
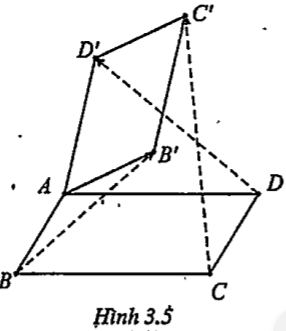
Bài 3.5. Trong không gian cho hai hình bình hành ABCD và AB’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ \[\overrightarrow{B{B}'},\overrightarrow{C{C}'},\overrightarrow{D{D}'}\] đồng phẳng.
| Lời giải Ta có: \[\overrightarrow{BB'}=\overrightarrow{AB'}-\overrightarrow{AB}\] (1) \[=\overrightarrow{D'C'}-\overrightarrow{DC}\] \[=\overrightarrow{DC'}-\overrightarrow{DD'}-\left( \overrightarrow{DC'}-\overrightarrow{C'C} \right)\] (2) \[=\overrightarrow{CC'}-\overrightarrow{DD'}\] (3) Chứng tỏ ba vectơ \[\overrightarrow{B{B}'},\overrightarrow{C{C}'},\overrightarrow{D{D}'}\] đồng phẳng.
| Giải thích Áp dụng quy tắc hiệu của hai vectơ cùng gốc, ta có (1). Để có (2), cần chú ý rằng ABCD là hình bình hành nên ta có: \[\overrightarrow{A{B}'}=\overrightarrow{D'{C}'}\], \[\overrightarrow{AB}=\overrightarrow{DC}\] Đẳng thức (3) chứng tỏ ba vectơ \[\overrightarrow{B{B}'},\overrightarrow{C{C}'},\overrightarrow{D{D}'}\] đồng phẳng.
|
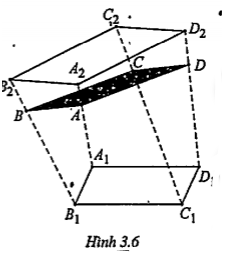
Bài 3.6. Trên mặt phẳng (α) cho hình bình hành A1B1C1D1. Về một phía đối với mặt phẳng (α) ta dựng hình bình hành A2B2C2D2. Trên các đoạn A1A2, B1B2, C1C2, D1D2 ta lần lượt lấy các điểm A, B, C, D sao cho \[\frac{A{{A}_{1}}}{A{{A}_{2}}}=\frac{B{{B}_{1}}}{B{{B}_{2}}}=\frac{C{{C}_{1}}}{C{{C}_{2}}}=\frac{D{{D}_{1}}}{D{{D}_{2}}}=3\]
Chứng minh rằng tứ giác ABCD là hình bình hành
| Lời giải \[\overrightarrow{AB}=\overrightarrow{A{{A}_{1}}}+\overrightarrow{{{A}_{1}}{{B}_{1}}}+\overrightarrow{{{B}_{1}}B}\] \[=\overrightarrow{A{{A}_{1}}}+\overrightarrow{{{D}_{1}}{{C}_{1}}}+\overrightarrow{{{B}_{1}}B}\] \[=\overrightarrow{A{{A}_{1}}}+\overrightarrow{{{D}_{1}}D}+\overrightarrow{DC}+\overrightarrow{C{{C}_{1}}}+\overrightarrow{{{B}_{1}}B}\] \[=\frac{3}{4}\overrightarrow{{{A}_{2}}{{A}_{1}}}+\frac{3}{4}\overrightarrow{{{D}_{1}}{{D}_{2}}}+\frac{3}{4}\overrightarrow{{{C}_{2}}{{C}_{1}}}+\frac{3}{4}\overrightarrow{{{B}_{1}}{{B}_{2}}}+\overrightarrow{DC}\] \[=(\frac{3}{4}\overrightarrow{{{A}_{2}}{{D}_{1}}}+\overrightarrow{{{D}_{1}}{{A}_{1}}})+\frac{3}{4}(\overrightarrow{{{D}_{1}}{{A}_{2}}}+\overrightarrow{{{A}_{2}}{{D}_{2}}})\] \[=\frac{3}{4}(\overrightarrow{{{C}_{2}}{{B}_{2}}}+\overrightarrow{{{B}_{2}}{{C}_{1}}})+\frac{3}{4}(\overrightarrow{{{B}_{1}}{{C}_{1}}}+\overrightarrow{{{C}_{1}}{{B}_{2}}})+\overrightarrow{DC}\]
\[=\frac{3}{4}(\overrightarrow{{{A}_{2}}{{D}_{1}}}+\overrightarrow{{{D}_{1}}{{A}_{2}}})+\frac{3}{4}(\overrightarrow{{{D}_{1}}{{A}_{1}}}+\overrightarrow{{{B}_{1}}{{C}_{1}}})\] \[=\frac{3}{4}(\overrightarrow{{{A}_{2}}{{D}_{2}}}+\overrightarrow{{{C}_{2}}{{B}_{2}}})+\frac{3}{4}(\overrightarrow{{{B}_{2}}{{C}_{1}}}+\overrightarrow{{{C}_{1}}{{B}_{2}}})\] \[\Rightarrow \overrightarrow{AB}=\overrightarrow{DC}\] Vậy ABCD là hình bình hành.
| Giải thích Ta thấy các điểm A, B, C, D không thẳng hàng nên để chứng minh tứ giác ABCD là hình bình hành, ta cần chứng minh \[\overrightarrow{AB}=\overrightarrow{DC}\] Phân tích \[\overrightarrow{AB}\] về theo vectơ \[\overrightarrow{DC}\] và tổng các vectơ mà áp dụng được giả thiết cho và áp dụng được quy tắc hình bình hành (hai hình bình hành A1B1C1D1 và A2B2C2D2)
Cần chú ý rằng các điểm A, B, C,D thuộc các đoạn thẳng \[{{A}_{1}}{{A}_{2}},{{B}_{1}}{{B}_{2}},{{C}_{1}}{{C}_{2}},{{D}_{1}}{{D}_{2}}\] nên \[\frac{{{A}_{1}}{{A}_{2}}}{A{{A}_{2}}}=3\Rightarrow \overrightarrow{A{{A}_{1}}}=3\overrightarrow{{{A}_{2}}A}=\frac{3}{4}\overrightarrow{{{A}_{2}}{{A}_{1}}}\] Tương tự, ta có: \[\overrightarrow{C{{C}_{1}}}=\frac{3}{4}\overrightarrow{{{C}_{2}}{{C}_{1}}}\] \[\overrightarrow{D{{D}_{1}}}=\frac{3}{4}\overrightarrow{{{D}_{2}}{{D}_{1}}}\], \[\overrightarrow{B{{B}_{1}}}=\frac{3}{4}\overrightarrow{{{B}_{2}}{{B}_{1}}}\]
|
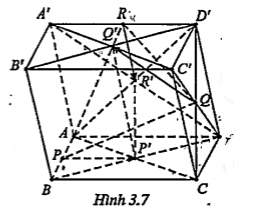
Bài 3.7. Cho hình hộp ABCD.A'B'C'D' có P và R lần lượt là trung điểm các cạnh AB và A'D'. Gọi P', Q, Q', R' lần lượt là tâm đối xứng của các hình bình hành ABCD, ADD'C', A'B'C'D', ADD'A'
a) Chứng minh rằng \[\overrightarrow{P{P}'}+\overrightarrow{Q{Q}'}+\overrightarrow{R{R}'}=\vec{0}\]
b) Chứng minh hai tam giác PQR và P'Q'R' có trọng tâm trùng nhau.
| Lời giải a) Chứng minh \[\overrightarrow{P{P}'}+\overrightarrow{Q{Q}'}+\overrightarrow{R{R}'}=\vec{0}\] Ta có: \[\overrightarrow{P{P}'}+\overrightarrow{Q{Q}'}+\overrightarrow{R{R}'}=\frac{1}{2}\overrightarrow{A\text{D}}+\frac{1}{2}\overrightarrow{DA'}+\frac{1}{2}\overrightarrow{DD'}\] \[=\frac{1}{2}(\overrightarrow{A\text{D}}+\overrightarrow{DA'})+\frac{1}{2}\overrightarrow{DD'}\]\[=\frac{1}{2}\overrightarrow{AA'}+\frac{1}{2}\overrightarrow{DD'}\] \[=\frac{1}{2}(\overrightarrow{AA'}+\overrightarrow{A'A})=\vec{0}\] | Giải thích
|
| b) Chứng minh hai tam giác... Gọi G,G’ tương ứng là trọng tâm của hai tam giác PQR và P’Q’R’. Ta có: \[3\overrightarrow{GG'}=\overrightarrow{G{P}'}+\overrightarrow{G{Q}'}+\overrightarrow{G{R}'}\] \[=\overrightarrow{GP}+\overrightarrow{PP'}+\overrightarrow{\text{GQ}}+\overrightarrow{QQ'}+\overrightarrow{GR}+\overrightarrow{R{R}'}\] \[=(\overrightarrow{GP}+\overrightarrow{\text{GQ}}+\overrightarrow{GR})+(\overrightarrow{QQ'}+\overrightarrow{PP'}+\overrightarrow{R{R}'})\] \[\Rightarrow \overrightarrow{\text{GG }\!\!'\!\!\text{ }}=0\Rightarrow G\equiv G'\] | • Để chứng minh hai điểm G và G’ trùng nhau, ta chứng minh \[\overrightarrow{GG'}=\overrightarrow{0}\] • Áp dụng tính chất trọng tâm của tam giác. |

.png)
.png)
.png)