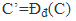Vấn đề 4. Dùng phép đối xứng để giải một số bài toán tìm tập hợp điểm
1. Phương pháp
Để tìm tập hợp điểm M’, ta làm như sau:
• Xác định phép đối xứng trục biến M thành M'.
• Tìm tập hợp của M.
• Suy ra tập hợp của M’.
2. Ví dụ
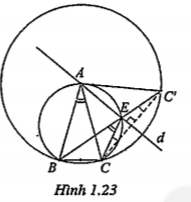
Ví dụ. Cho tam giác ABC cân tại A. Một đường thẳng d thay đổi, nhưng luôn đi qua A. Gọi C’ là điểm đối xứng của C qua đường thẳng d. Đường thẳng BC’ cắt d tại E. Hãy xác định tập hợp của các điểm C’ và E.
| Lời giải • Tập hợp của C': Vì nên AC’=AC (không đổi) nên tập hợp của C’ là đường tròn bán kính AC. • Tập hợp của E: Vì \[E\in d\] nên \[\widehat{EC'C}=\widehat{ECC'}\] (1) \[\Delta ECC'\] cho : \[\widehat{EC'C}+\widehat{ECC'}=\widehat{BEC}\] \[2\widehat{EC'C}=\widehat{BEC}\] (2) Trong đường tròn (A,AC), ta có \[\widehat{BAC}=2\widehat{EC'C}\] (3) (2) và (3) \[\Rightarrow \widehat{BEC}=\widehat{BAC}\] Vậy tập hợp của E là cung chứa góc dựng trên cạnh BC. | Giải thích • Để có (2), ta áp dụng tính chất: Trong một tam giác, số đo của góc ngoài bằng tổng số đo của hai góc trong không kề với nó.
• Để có (3), ta áp dụng tính chất: Trong đường tròn, số đo của góc nội tiếp bằng nửa số đo của góc ở tâm cùng chắn một cung.
|