C. CÂU HỎI VÀ BÀI TẬP
Bài 2.22. Cho tứ diện ABCD. Gọi G1, G2, G3 lần lượt là trọng tâm của các tam giác ABC, ACD, ABD. Chứng minh rằng (G1G2G3)//(BCD).
Đề nghị độc giả xem bài giải chi tiết tương tự tại ví dụ của vấn đề 1.
Bài 2.23. Từ bốn đỉnh của hình bình hành ABCD vẽ bốn nửa đường thẳng song song cùng chiều Ax, By, Cz và Dt sao cho chúng cắt mặt phẳng (ABCD). Một mặt phẳng (\[\alpha \]) cắt bốn nửa đường thẳng nói trên tại A’, B’, C’ và D’.
a) Chứng minh rằng (Ax, By)//(Cz,Dt) và (Ax, Dt)//(By, Cz).
b) Tứ giác A’B’C’D’ là hình gì?
c) Chứng minh AA’+ CC’ = BB' + DD”
| Lời giải a) Chứng minh (Ax, By)//(Cz,Dt) Ta có
\[\Rightarrow \] (Ax, By)//(Cz,Dt) Tương tự , ta có: (Ax,Dt)//(By,Cz). | Giải thích Áp dụng định lý 11
|
| b) Hình tính tứ giác A’B’C’D’ Ta có: \[\Rightarrow A'B'//C'D'\] (1) Tương tự, ta có: A'D'// B’C’ (2) (1) và (2)\[\Rightarrow \] A'B'C'D' là hình bình hành. | Áp dụng định lí 11, ta chứng minh tứ giác A’B’C’D’ có các cặp cạnh đối song song. |
| c) Chứng minh... Gọi II’ lần lượt là tâm của hai hình bình hành ABCD và A'B'C'D. Tứ giác ACC'A' là hình thang có II’ là đường trung bình nên: \[II'=\frac{AA'+CC'}{2}\] (1) Tương tự, ta có: \[II'=\frac{BB'+DD'}{2}\] (2) (1) và (2)\[\Rightarrow \] AA'+CC' =BB'+DD'.
| Nhắc lại: Đoạn thẳng nối trung điểm của hai cạnh bên của hình thang là đường trung bình của hình thang. Độ dài đường trung bình của hình thang bằng nửa tổng độ dài hai đáy của hình thang ấy. |
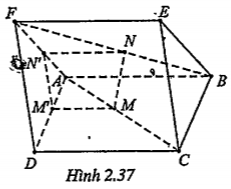
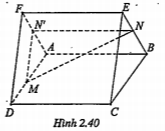
Bài 2.24. Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng phân biệt. Trên các đường chéo AC và BF lần lượt lấy các điểm M và N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD và AF tại M’, N’. Chứng minh:
a) (ADF)//(BCE).
b) M'N'//DF.
c) (DEF) // (MM'N’N) và MN // (DEF).
| Lời giải a) Chứng minh (ADF)//(BCE) Ta có: AD//BC, AF//BE \[\Rightarrow \](ADF)//(BCE) |
|
| b) Chứng minh M’N’ // DF Та có:
\[\Rightarrow \frac{AN'}{AF}=\frac{AM'}{AD}\Rightarrow M'N'//DF\] | Do hai hình vuông ABCD và ABEF có cạnh bằng nhau nên hai đường chéo AC và BF cũng bằng nhau.
|
| c) Chứng minh (DEF) // (MM'N'N) Ta có: DF//M’N’ FE//NN’ \[\Rightarrow \] (DEF) // (MM'NN’) |
|
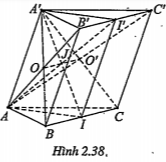
Bài 2.25. Cho hình lăng trụ tam giác ABC.A'B'C' có các cạnh bên là AA', BB’, CC’. Gọi I và I’ tương ứng là trung điểm của hai cạnh BC và B’C’.
a) Chứng minh rằng AI//A’I’.
b) Tìm giao điểm của IA’ với mặt phẳng (AB’C’).
c) Tìm giao tuyến của (AB’C’) và (A'BC).
| Giải thích a) Chứng minh AI// A’I’ I là trung điểm của BC I’ là trung điểm của B’C’ \[\Rightarrow \]II’ là đường trung bình của hình bình hành BCC'B' nên II'//BB'\[\Rightarrow \]II'//AA'\[\Rightarrow \]\[\exists \] (AA', II'). Ta có: (ABC)//(A'B'C') (AA',II')\[\cap \] (ABC)=AI (AA', II')\[\cap \] (A'B'C') = A'I’ => AI//A'I’ | Lời giải
|
| b) Giao điểm của IA’ với (AB’C’) . Ta có: (AA', II')\[\supset \] IA’ (AA',II')\[\cap \] (AB'C')=AI'. Trong (AA',II'): AI'\[\cap \]IA’ =J \[\Rightarrow J\in IA'\cap \left( AB'C' \right)\] | Cách tìm giao điểm của đường thẳng với mặt phẳng: Xem lại phương pháp tại vấn đề 2, bài1.
|
| c) Giao tuyến của (AB’C’) và (A’BC) Gọi \[O\in A'B\cap AB',O'\in CA'\cap AC'\] thì (AB'C')\[\cap \] (A'BC)=OO'. |
|
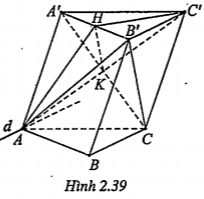
Bài 2.26. Cho hình tăng trụ tam giác ABC.A’B’C’. Gọi H là trung điểm của A'B'.
a) Chứng minh rằng CB’//(AHC’)
b) Tìm giao tuyến d của (AB’C’) và (ABC).
| Lời giải a) Chứng minh CB'//(AHC') Gọi \[K\in CA'\cap AC'\]. Khi đó: \[CB'//HK\] \[HK\subset \left( AHC' \right)\Rightarrow CB'//\left( AHC' \right)\] | Giải thích H và K lần lượt là trung điểm của A'B' và CA’ nên HK là đường trung bình của tam giác A'BC. |
| b) Giao tuyến d=(AB’C’)\[\cap \] (ABC) Ta có: (AB'C')\[\supset \] B'C' (ABC)\[\supset \] BC B'C' // BC A\[\in \] (AB'C')\[\cap \] (ABC) \[\Rightarrow \]d qua A d//BC//B'C' |
|
Bài 2.27. Cho hai hình bình hành ABCD, ABEF không cùng nằm trong một mặt phẳng. Gọi M và N là hai điểm di động tương ứng trên AD và BE sao cho \[\frac{AM}{MD}=\frac{BN}{NE}\] . Chứng minh rằng đường thẳng MN luôn luôn đi qua một mặt phẳng cố định. Hãy chỉ ra mặt phẳng cố định đó.
| Giải thích Vē NN' // AB (N'\[\in \]AF), ta có: \[\frac{BN}{NE}=\frac{AN'}{N'F}\] (1) Mặt khác: \[\frac{AM}{MD}=\frac{BN}{NE}\] (2) (1) và (2) \[\Rightarrow \frac{AN'}{N'F}=\frac{AM}{MD}\Rightarrow MN'//DF\] Như vậy: NN'//AB MN'//DF \[\Rightarrow \] (MNN’)//(DEF) mà MN\[\subset \](MNN’) \[\Rightarrow \]MN//(DEF) cố định. | Giải thích
Chú ý. • Cho hai mặt phẳng song song. Khi đó, bất kì đường thẳng nào nằm trong mặt phẳng này đều song song với mặt phẳng kia. • Vì hai hình bình hành ABDE và ABEF cố định nên mặt phẳng (DEF) cố định.
|
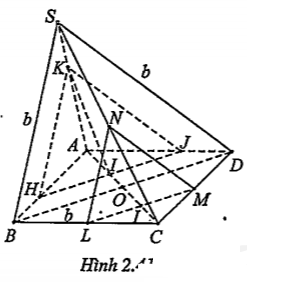
Bài 2.28. Cho hình chóp S.ABCD có đáy là hình bình hành ABCD, O là giao điểm của hai đường chéo, AC = a, BD = b, tam giác SBD đều. Gọi I là điểm di động trên đoạn AC với AI= x (0 < x < a). Lấy \[\left( \alpha \right)\] là mặt phẳng đi qua I và song song với mặt phẳng (SBD).
a) Xác định thiết diện của mặt phẳng \[\left( \alpha \right)\] với hình chóp S.ABCD.
b) Tìm diện tích S của thiết diện ở câu a) theo a, b, x. Tìm x để S lớn nhất.
| Giải thích a) Thiết diện của \[\left( \alpha \right)\] với hình chóp Ta xét ba trường hợp: • Trường hợp 1.
\[\left( \alpha \right)\cap \left( SAB \right)=HK\] Vậy thiết diện cần tìm là tam giác HJK. • Trường hợp 2: \[I\equiv 0\left( x=\frac{a}{2} \right)\] Khi \[I\equiv O\] thì \[H\equiv B,J\equiv D,K\equiv S\] nên thiết diện cần tìm là tam giác SBD. • Trường hợp 3: Làm tương tự trường hợp \[I\in OA\], ta có: thiết diện cần tìm là tam giác LMN. | Giải thích Ta tìm các đoạn giao tuyến của \[\left( \alpha \right)\] với các mặt của hình chóp nhờ áp dụng định lí 11. Cần chú ý đến giả thiết là I di động trên AC nên ta cần phải xét ba trường hợp như trên.
|
| b) Diện tích của thiết diện • Diện tích
mà BD=SB=b nên HJ = HK (1) Tương tự , ta có:HJ =JK (2) (1) và (2)\[\Rightarrow \] HJ= HK =JK nên tam giác HJK đều. Ta có: \[\frac{AI}{AO}=\frac{HJ}{BD}\Rightarrow \frac{x}{\frac{a}{2}}=\frac{HJ}{b}\Rightarrow HJ=\frac{2bx}{a}\] Vậy: \[{{S}_{HJK}}=\frac{1}{2}.{{\left( \frac{2bx}{a} \right)}^{2}}.\sin {{60}^{0}}=\frac{{{b}^{2}}{{x}^{2}}\sqrt{3}}{{{a}^{2}}}\] • Diện tích \[{{S}_{SBD}}=\frac{1}{2}.{{\left( b \right)}^{2}}.\sin {{60}^{0}}=\frac{{{b}^{2}}\sqrt{3}}{4}\] • Diện tích Tương tự, tam giác LMN là tam giác đều. Ta có: \[\frac{CI}{CO}=\frac{LM}{BD}\] \[\Rightarrow \frac{a-x}{\frac{a}{2}}=\frac{LM}{b}\Rightarrow LM=\frac{2b(a-x)}{a}\] Vậy: \[{{S}_{LMN}}=\frac{1}{2}.\left( \frac{2b(a-x)}{a} \right).\sin {{60}^{0}}=\frac{{{b}^{2}}\sqrt{3}{{\left( a-x \right)}^{2}}}{{{a}^{2}}}\] Tóm lại: Diện tích của thiết diện =
| Hướng dẫn: • Chứng minh thiết điện là tam giác đều. • Để tính diện tích thiết diện (là tam giác), ta đã áp dụng công thức: \[S=\frac{1}{2}bc.\sin A\] Ở đây thiết diện là tam giác đều nên ta có: b=c, sinA =sin 60°.
|
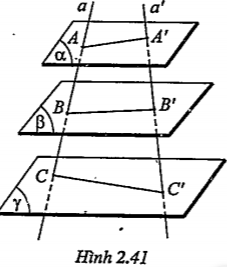
Bài 2.29. Cho ba mặt phẳng \[\left( \alpha \right),\left( \beta \right),\left( \gamma \right)\]song song với nhau. Hai đường thẳng a và a' cắt ba mặt phẳng ấy theo thứ tự nói trên tại A, B, C và A’, B’, C’. Cho AB = 5, BC=4, A’C’ = 18. Tính độ dài A’B’, B’C’.
| Giải thích Theo định lí Thales, ta có: \[\frac{AB}{A'B'}=\frac{BC}{B'C'}\Rightarrow \frac{5}{A'B'}=\frac{4}{B'C'}\] \[\Rightarrow \frac{B'C'}{A'B'}=\frac{4}{5}\Rightarrow \frac{B'C'+A'B'}{A'B'}=\frac{9}{5}\] \[\Rightarrow \frac{A'C'}{A'B'}=\frac{9}{5}\Rightarrow \frac{18}{A'B'}=\frac{9}{5}\Rightarrow A'B'=10\] Ta có: \[B'C'=A'C'-A'B'=18-10=8\] Vậy: \[A'B'=10,B'C'=8\] |
|
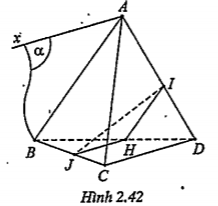
Bài 2.30: Cho tứ diện ABCD. Gọi I, J là hai điểm di động trên các cạnh AD và BC sao cho \[\frac{IA}{ID}=\frac{JB}{JC}\]. Chứng minh rằng IJ luôn luôn song song với một mặt phẳng cố định.
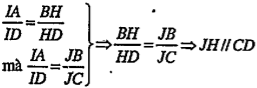
| Giải thích Vẽ IH//AB (H\[\in \]BD). Ta có:
Vẽ Ax//CD. Khi đó tồn tại mặt phẳng (Ax,AB). Ta có: JH // Ax (//CD) IH//AB mà \[IJ\subset \left( IJH \right)\] \[\Rightarrow \left( IJH \right)//\left( Ax,AB \right)\] \[\Rightarrow \]IJ//(Ax,AB) cố định | Giải thích.
Chú ý. Vì AB, CD cố định nên (Ax, AB) cố định. |
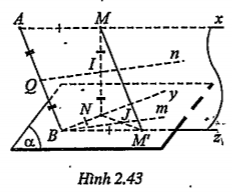
Bài 2.31. Cho hai tia Ax, By chéo nhau. Lấy M, N lần lượt là các điểm di động trên Ax, By. Gọi \[\left( \alpha \right)\]là mặt phẳng chứa By và song song với Ax. Đường thẳng qua M và song song với AB cắt \[\left( \alpha \right)\] tại M'.
a) Tìm tập hợp điểm M’.
b) Gọi I là trung điểm của MN. Tìm tập hợp các điểm I khi AM = BN.
| Giải thích a) Tập hợp của M' Ta có:(Ax, AB)\[\cap \left( \alpha \right)=Bz//Ax\] mà Vậy khi M di động trên tia Ax thì M' chạy trên tia Bz | Nhắc lại định lí 5, bài 3
|
| b) Tập hợp của I Tứ giác ABM’M là hình bình hành nên AM=BM' mà AM=BN\[\Rightarrow BM'=BN\] \[\Rightarrow \Delta \]BNM' cân tại B. Gọi J là trung điểm của NM' thì Bm (qua J) là phân giác của góc Khi M di động trên Ax thì J chạy trên tia Bm
IJ là đường trung bình của \[\Delta \]NMM’ nên IJ // MM' (1) IJ=\[\frac{1}{2}\] MM’ (2) Mà MM'//AB (3) MM'=AB (4) (1), (3)\[\Rightarrow \] JI//AB (2), (4)\[\Rightarrow \]IJ=\[\frac{1}{2}\]AB \[\Rightarrow \] BJIQ là hình bình hành (Q là trung điểm của AB). Suy ra \[\overrightarrow{IJ}=\overrightarrow{BQ}\Rightarrow I={{T}_{\overrightarrow{BQ}}}(J)\] Vậy tập hợp của I là tia Qn song song với tia Bm. |
|

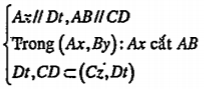
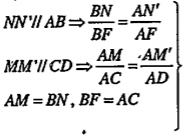
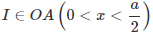
.png)
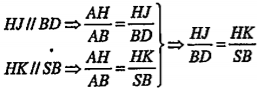
.png)
.png)
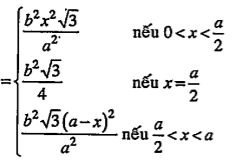
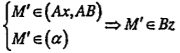
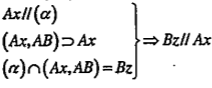
.png)