Câu hỏi và bài tập

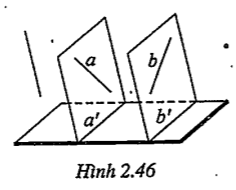
Lời giải

• Giả sử a, b là hai đường thẳng chéo nhau có hình chiếu lần lượt là a’, b’.

Nếu mặt phẳng (a,a’)//(b,b’) thì các giao tuyến a’ và b’ cũng song song với nhau.

Vậy hình chiếu của hai đường thẳng chéo nhau có thể song song với nhau.

• Giả sử m và n là hai đường cắt nhau tại M có hình chiếu lần lượt là m’, n’ và M’. Khi đó:

\[M'\in m',M'\in n'\Rightarrow M'\in m'\cap n'\]

nghĩa là m’ và n’ cắt nhau tại M’.

Vậy hình chiếu của hai đường thẳng cắt nhau không thể song song với nhau.

Ta cần chú ý rằng hình biểu diễn phải giữ nguyên tính thuộc. Nghĩa là M thuộc m và n thì M’ thuộc m’ và n’.

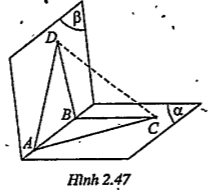
Lời giải

Trong mặt phẳng (\[\alpha \]), ta vẽ tam giác ABC bất kì. Trong mặt phẳng (\[\beta \]) khác (\[\alpha \]), ta vẽ tam giác đều ABD. Khi đó tam giác ABC có thể xem là hình chiếu của tam giác đều ABD theo phương chiếu DC lên mặt phẳng (\[\alpha \]).

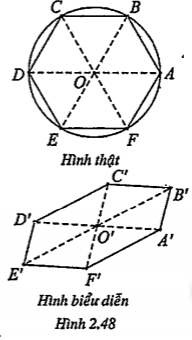
Lời giải

Giả sử trên hình thật ta có lục giác đều ABCDEF tâm O.

• OABC là hình thoi.

• Các đỉnh D, E, F lần lượt đối xứng với A, B, C qua tâm O.

Từ đó suy ra cách vẽ hình biểu diễn A’B’C’D’E’F’ như sau:

+ Vẽ hình bình hành O’A'B'C’ biểu diễn hình thoi OABC.

+ Lấy D’, E’, F’ lần lượt đối xứng với A’, B’, C’ qua O. Khi đó A’B’C’D’E’F’ là hình biểu diễn của lục giác đều ABCDEF.

Đề nghị độc giả xem ví dụ b, trong phần dạng toán cơ bản.

Lời giải .

Giả sử ta có tứ diện ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD.

• E, F lần lượt là hình chiếu của A,C trên mặt phẳng chiếu (\[\alpha \]).

• G, H lần lượt là hình chiếu của B,D trên mặt phẳng chiếu (\[\alpha \]).

• Để tứ giác EFGH là hình bình hành thì ta phải có O là trung điểm của hai đường chéo EG và FH.

Nếu gọi M, N lần lượt là trung điểm của AB, CD thì hình chiếu của M, N trên (\[\alpha \]) phải trùng với O. Từ đó suy ra phương chiếu phải song song với MN.

Vậy để hình chiếu của một tứ diện là một hình bình hành thì:

i) Phương chiếu d song song với đường thẳng đi qua trung điểm của hai cạnh đối.

ii) Mặt phẳng chiếu là mặt phẳng tùy ý nhưng phải cắt d.