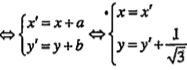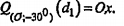Vấn đề 1. Xác định ảnh của một hình qua phép đồng dạng

Lời giải

• Áp dụng biểu thức tọa độ của phép tịnh tiến, ta có:

\[M'(x';y')={{T}_{\overrightarrow{v}}}(M)\]

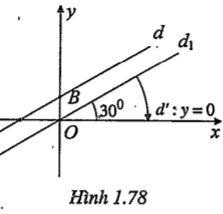
Giải thích

Các bước thực hiện:

• Bước 1: Tìm ảnh d1 của d qua phép tịnh tiến vectơ cho trước.

• Bước 2: Tìm ảnh d' của d1 qua phép quay đã cho. Khi đó, phương trình của d’ là phương trình cần tìm

Nhắc lại.

Đường thẳng d: Ax + By + C = 0 có vectơ chỉ phương\[\overrightarrow{u}=\left( -B;A \right)\]. Khi đó hệ số góc của đường thẳng là \[\tan \varphi =-\frac{A}{B}\] với \[\varphi \] là góc giữa d với trục Ox. Với nhận xét này, ta thấy phép quay \[{{Q}_{(O,-{{30}^{0}})}}\] biến d1 thành trục hoành Ox: y = 0.

Thay vào phương trình của d, ta có:

\[x'-\sqrt{3}\left( y'+\frac{1}{\sqrt{3}} \right)+1=0\]

\[\Leftrightarrow x'-\sqrt{3}y'=0\]

Vậy ảnh của d là đường thẳng d1 có phương trình d1 : \[x-\sqrt{3}y=0\]

• Đường thẳng d1 có vectơ chỉ phương là \[\overrightarrow{u}=\left( \sqrt{3};1 \right)\] nên có hệ số góc :\[k=\frac{1}{\sqrt{3}}\Leftrightarrow \tan \phi =\frac{1}{\sqrt{3}}\Leftrightarrow \phi ={{30}^{0}}\]

(với \[\phi =({{d}_{1}},Ox)\])

Do đó:

Vậy phương trình của d' là y=0