B. DẠNG TOÁN CƠ BẢN
Vấn đề 1. Xác định ảnh của một hình qua phép đối xứng trục
1. Phương pháp
Để xác định ảnh của một hình qua phép đối xứng trục d, ta có thể dùng các phương pháp sau:
• Dùng định nghĩa của phép đối xứng trục.
• Dùng biểu thức vectơ của phép đối xứng trục:
.png) \[\Leftrightarrow \overrightarrow{{{M}_{0}}M'}=-\overrightarrow{{{M}_{0}}M}\]
\[\Leftrightarrow \overrightarrow{{{M}_{0}}M'}=-\overrightarrow{{{M}_{0}}M}\]
• Dùng biểu thức tọa độ của phép đối xứng qua các trục tọa độ Ox, Oy.
Ví dụ 1. Cho tứ giác ABCD. Gọi E là trung điểm của BC. Xác định ảnh của tam giác CDE qua phép đối xứng qua đường thẳng AB.
| Lời giải Ta có:
(đường thẳng AB là trung trực của CC’, DD’, EE') Vậy | Giải thích
|
Ví dụ 2. Trong mặt phẳng Oxy cho điểm M(-1;2) và đường thẳng d: x-y-2=0.
a) Xác định ảnh của M qua phép đối xứng trục Ox, Oy
b) Xác định ảnh của M qua phép đối xứng qua đường thẳng d.
| Lời giải a) Ta có:
| Giải thích Áp dụng biểu thức tọa độ của phép đối xứng trục Ox, Oy |
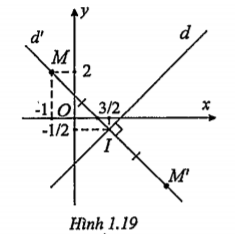
| b) Gọi d’ là đường thẳng đi qua M và vuông góc với d. Ta có:
\[\Rightarrow d':1(x+1)+1(y-2)=0\] \[\Leftrightarrow d':x+y-1=0\] Gọi \[I\in d\cap d'\]thì tọa độ của I là nghiệm của hệ d và d’:
| • Phương trình đường thẳng đi qua điểm
• Đường thẳng d: Ax+By+C=0 có một vectơ chỉ phương là \[\overrightarrow{u}=(A;B)\] • Đường thẳng d’ đi qua • \[\overrightarrow{IM'}=({{x}_{M'}}-{{x}_{I}};{{y}_{M'}}-{{y}_{I}})\] • \[\overrightarrow{IM'}=-\overrightarrow{IM}\]
|
.png)
Ví dụ 3. Trong mặt phẳng Oxy cho hai đường thẳng d: 2x-y+4=0 và d1: x+y-1=0.
a) Tìm ảnh d’ của d qua phép đối xứng trục Oy .
b) Viết phương trình đường thẳng d1’ là ảnh của d1 qua phép đối xứng qua đường thẳng d.
| Lời giải \[A\in d\cap Ox\Rightarrow A(-2;0)\] \[B\in d\cap Oy\Rightarrow A(0;4)\] Ta có:
Khi đó
\[\Rightarrow d':2(x-2)+y=0\] Vậy phương trình của d’ là: 2x+y-4=0 | Giải thích Để tìm ảnh d’ của đường thẳng d qua phép đối xứng trục Oy, ta tìm một điểm bất kì trên d (thường lấy giao điểm của d với trục Ox) rồi tìm ảnh của điểm đó qua phép đối xứng trục Oy. Khi đó đường thẳng d’ đi qua hai điểm A’ và B (với B là giao điểm của d với Oy) Nhắc lại cách viết phương trình đường thẳng đi qua hai điểm cho trước: (xem lại Hình học 10)
|
| b) Gọi \[I\in d\cap {{d}_{1}}\]thì tọa độ của I là nghiệm của hệ:
\[\Rightarrow I(-1;2)\] | Để tìm ảnh d’1 của d1 qua phép đối xứng trục d (d và d1 cắt nhau tại I), ta làm như sau: • Tìm tọa độ giao điểm I của d và d1 |
| Lấy \[D(0;1)\in {{d}_{1}}\]. Gọi
\[\Rightarrow DD':x+2y-2=0\] Gọi \[J\in DD'\cap d\] thì tọa độ của J là nghiệm của hệ:
Ta có: \[\overrightarrow{JD'}=\overrightarrow{DJ}\]
\[\Rightarrow {{d}_{1}}:(x+1)+7(y-2)=0\]
Vậy phương trình của d1’ là: x+7y-13=0 | • Lấy trên d1 điểm D tùy ý. Viết phương trình đường thẳng đi qua D và vuông góc với d. Tìm tọa độ giao điểm J của đường thẳng này với d. • Gọi D’ là ảnh của D qua phép đối xứng trục d thì J là trung điểm của DD’. Từ đó suy ra tọa độ của D’. • Đường thẳng d’1 đi qua hai điểm D’ và I. Ta có: \[\overrightarrow{JD'}=\left( {{x}_{D'}}+\frac{6}{5};{{y}_{D'}}-\frac{8}{5} \right)\] \[\overrightarrow{DJ}=\left( -\frac{6}{5};\frac{3}{5} \right)\] Chú ý. Nếu d và d1: Ax + By + C = 0 (với A, B, C cho trước) song song thì ta làm như sau: • Phương trình đường thẳng d1’ có dạng: Ax + By + C = 0. • Lấy trên d1 một điểm A tùy ý. Xác định ảnh A’ của A qua trục đối xứng d. • Thay tọa độ của A’ vào phương trình d1’ để tính C’. Từ đó suy ra phương trình của d1’ |

.png)
.png) \[(\Delta CDE)=\Delta C'D'E'\]
\[(\Delta CDE)=\Delta C'D'E'\] 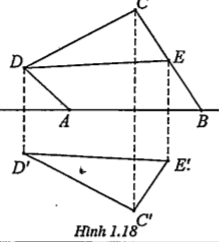
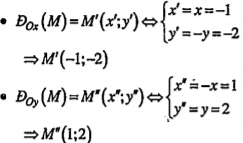

.png) và nhận vectơ
và nhận vectơ .png) làm vectơ pháp tuyến có dạng:
làm vectơ pháp tuyến có dạng:.png)
.png) và vuông góc với d thì nhận vectơ chỉ phương của d làm vectơ pháp tuyến.
và vuông góc với d thì nhận vectơ chỉ phương của d làm vectơ pháp tuyến.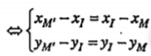
.png)
.png) thì d’ đi qua hai điểm A’ và B.
thì d’ đi qua hai điểm A’ và B.

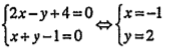
.png)
.png)
.png)
.png)